Eric Weinstein first presented Geometric Unity in three lectures delivered over the course of a week at the University of Oxford by invitation of Marcus du Sautoy, the Simonyi Professor for the Public Understanding of Science. The lectures provided a broad overview of the mathematical structures in the theory’s endogenous version, discussed where current effective theories are recovered in those structures, and showed general predictions based on those structures.
“A Portal Special Presentation- Geometric Unity: A First Look” was uploaded on April 2nd, 2020 as a general introduction to Geometric Unity. The video is divided into three sections: a preface, the lecture proper, and a supplementary PowerPoint presentation. The preface provides context based on historical and contemporary events and introduces the concept of a theory of everything. The lecture shown is a recording of the first lecture given at the University of Oxford. The PowerPoint reviews the lecture’s major concepts in a more up-to-date notation.
Table of Contents
- Preface
- Lecture at the University of Oxford
- Powerpoint
- Closing Thoughts
Transcript
Preface
00:00:00
Eric Weinstein: Hello, you’ve found The Portal. I’m your host, Eric Weinstein, and I think that today’s must be the most unusual episode yet of a podcast that has been marked by almost regular unusual episodes. Now, this is the first podcast that I’m recording at home. I don’t really have a home recording studio, so we’re really doing this from chicken wire and masking tape. But, I am sheltering in place because of the worldwide COVID pandemic, and what we’ve been asked by the state of California and by the federal government is to shelter in place for an upcoming month, because today is April 1st. Now during a pandemic, I can assure you that no one is interested in April Fool’s jokes. So the question is what to do with the April Fool’s tradition in a situation in which nobody wants a prank.
00:00:47
I thought that this was probably the best time to launch an idea that I’ve been playing with for years. And that idea is that it is dangerous to have a world in which we are afraid to talk about what we think is true. When I think about what happened during the beginning of the COVID pandemic, I find that we were, in general, intimidated from sharing our fears about the virus. We were told that if we wore masks we were acting in a peculiar fashion, if we refused to shake hands we were behaving in a strange and unpleasant social way. We did not want to be alarmist, we did not want to be seen as Chicken Little. And in fact, it was extremely important that we not be seen as xenophobic, given that the outbreak was originating in Wuhan, China. In fact, perhaps the most dangerous idea was that this outbreak might have been connected to some research being done in a lab, perhaps a bioweapons lab. We really don’t know where this epidemic began. What is the etiology of something that is causing the entire world economy to effectively shut down? What I believe is that that silence has been deadly. We have many people who have now lost their lives because we did not feel free to exchange ideas, to think, and to talk. And in fact, many of the people who warned us first were the freest members of society, having been previously canceled by standard mainstream institutions and their associated media.
00:02:17
So what I thought would be important for an April Fool’s Day that no one wants to actually participate in was to deal with an idea that, maybe one day a year, we should all be free to share crazy ideas that are going around between our ears and in our head. We’re having conversations with ourselves, wondering, ‘Is anyone else seeing the same thing that I’m seeing?’ But we are too afraid, because the social stigma for actually believing in things—that maybe things are possible, or perhaps there’s a conspiracy somewhere, perhaps we are ill-prepared… For example, I believe that our current pandemic is exacerbated because our government and our readiness czars failed to stock adequate supplies, and that these supplies were called for in the academic literature for years. There was absolutely no excuse not to have personal protective equipment stocked for doctors and nurses and hospitals, to say nothing of all of the people who are on the front lines of treating patients sick with COVID. Now, currently, I don’t believe that you can trust the World Health Organization. Absolutely not. I don’t think you can trust the Surgeon General of the United States, and I absolutely don’t think you can trust the CDC, because they are all covering for our inadequacy. This was a problem that we always knew was coming. And we at one point had stocks, which apparently were depleted under a previous administration and not restocked under this administration. In fact, our fear of dealing with a pervasive institutional incompetence has blinded us to the degradation in our society across all major institutions. As I’ve discussed before on the program, I believe that this has a singular etiology. That is, that because of embedded growth obligations coming from the previous era of unsustainable post-war growth, from about 1945 to 1971, ’73, something like that, we built in expectations to our system that cannot currently be met. We will not have technology that follows the same breakneck pace of innovation. As a result, we have a system whereby the heads of our organizations are forced to cover for their inadequacies because growth is built into the system that cannot be sustained. Therefore, there is not the funding, the manpower—there is not the wherewithal to continue many of our programs because we do not actually have the ability to continue to simply grow our way out. At least, so far.
00:04:48
So, what’s today’s program about? Well, I thought that what I would do is to let go of something that I’ve been keeping pretty close, for I think about 37 years. When I was around 19, I started… this is hard to talk about. When I was around 18 or 19, I was at the University of Pennsylvania, and I thought I saw a glimmer of hope. I thought I saw that some new equations that were being played with might actually provide a solution to some of the problems that had bedeviled Einstein and others for years in the quest for a unified field theory. Now, it’s an embarrassing thing to say that one is a unified field theorist. It is effectively equivalent to saying I’m interested in perpetual motion machines, or that I have a private cure for cancer that I’m trying on rabbits in my backyard. However, I actually think that it’s important to fess up, because that’s exactly what this is. Now, in my situation, I have an extremely unusual history, and I really don’t want to get bogged down in all of the things that happened while I was a student trying to develop this theory, because it is not a particularly happy story. I believe that this theory is an incredibly joyous one.
What a Theory of Everything Means
00:06:15
Now, in this situation, I want to talk about what it means to have a theory of everything. We’ve never seen one. And in fact, not only have we never seen a theory of everything, we’ve never even seen, I believe, a candidate for a theory of everything. And because a theory of everything would have to have different characteristics than, I believe, every theory that has gone before, we don’t think enough about what the difference is between what we would normally call in physics an effective theory and a fundamental one. Now, if you’re familiar with the M.C. Escher drawing called Drawing Hands, it is a lithograph of two hands apparently drawing each other into existence on some kind of a canvas or piece of paper. That is sometimes referred to as a strange loop, but it in fact is an attempt to answer the question, “What is the fire that lights itself?” This is the problem that bedevils us when we search for a unified theory that doesn’t bedevil us, in my opinion, in any previous effective theory.
00:07:25
Now, why is that? Well, many people confuse a theory of everything, as if they imagine that it’s a theory in which you can compute every eventuality, and it is absolutely not that, because the computational power is very different than the question of whether or not the rules are effectively given. I’ve analogized it to a game of chess, and knowing all of the rules is equivalent to a theory of everything. Knowing how to play chess well is an entirely different question. But in the case of a theory of everything, or a unified field theory if you will, many people also take it to be an answer to the question, “Why is there something rather than nothing?” And I don’t think that this is, in fact, what a theory of everything is meant to be either. Now, why is that? Well, because I believe at some level it is impossible for most of us to imagine an airtight argument, mathematically speaking, which coaxes out of an absolute void a something. However, there’s a different question which I think might actually animate us, and which is the right question to ask of a potential candidate. And that is, “How does one get everything from almost nothing?” In the M.C. Escher drawing or lithograph, Hands Drawing Hands, or Drawing Hands, what we see is that the paper is presupposed. That is, if you could imagine a theory of everything, it would be like saying, “If I posit the paper, can the paper will the ink into being, such that the ink gives rise to the pens, and the pens draw the hands, which in fact manipulate the pens to use the ink?” That kind of a problem is one which is of a very different character than everything that has gone before. It is also, in my opinion, an explanation of why the physics community has been stalled for nearly 50 years since around 1973, when the Standard Model was intellectually in place.
00:09:26
Now, consider this: we have never had, in modern times, a drought where no person working in pure fundamental theory has taken a trip to Stockholm—just as a rough indicator—for contributing to the Standard Model. No one, in my opinion, since let’s see, Frank Wilczek, who was born in 1951—no one born after that time has in fact contributed to the Standard Model in a clear and profound way. That is not to say that no work has been done, but for the most part, the current generation of physicists has, for more than 40 years and almost 50 years, remained stagnant within the standard paradigm of physics, which is positing theories that are then verified by experiment. Now my belief, which is relatively radical, is that there is no way to get to our final destination using the tools that have gotten us to where we are now. In other words, what got you here cannot get you there.
The Political Economy of Science
00:10:25
And in particular, one of the biggest problems we have is the political economy of science. We have effectively starved our scientific enterprise for resources, creating a dire and cutthroat competition which has completely deranged the scientific tradition. And so, one of the things that’s going to happen in this lecture is that I’m simply going to announce that I have broken, and have broken for many years, with just about every expectation of standard science. That is not to say that the equations or the style of presentation is going to be foreign. Quite the contrary. I have every intention of writing up some results, in standard terminology wherever possible, using popular mathematical type-setting programs. But it goes far deeper than this. My belief is that what we’ve created is a career structure, a journal structure, an employment structure, and access structure that cannot possibly complete the job. And why is that? Well, what if, in the last leg, in fact, we had a situation by which an attempt at the fundamental theory would result almost certainly in career suicide? Now, if you think of that as an explanation, you would realize that it has the power to synchronize failure across many seemingly independent experiments. And I believe that that’s exactly what’s been going on through the so-called string theory revolutions, one, two, and perhaps three.
00:11:57
Now in that case, what happened was a theory became fixed in the minds of, really, the Baby Boom generation of physicists, because it allowed for infinite elaboration within a mathematical, or more particularly, a geometric context. And those supposed physicists spent their time submitting papers to what’s called the High Energy section of the so-called preprint arXiv, but in fact, most of these papers have nothing to do with high energy physics whatsoever. And if you’re looking for the designation, it’s hep-th, High Energy Physics – Theory. Now, if you look through those papers, they don’t seem to have much to do with particles. They don’t seem to have to do with forces and spacetime. They seem to have to do with very strange and obscure mathematical issues. And in the years since the string theory program got particularly reanimated, I guess that would be around 1984 with the anomaly cancellation of Green and Schwarz, what you’ll find is that physics became very active and simultaneously ground to a halt. It failed to remain a physical subject. It became something like a medieval quest for the number of angels to dance on the head of a pin.
00:13:14
Now, in this circumstance, I think it’s very important to realize that this is not a paper, and we are not submitting to the arXiv. In fact, the arXiv requires people who are not employed at universities to get permission from some member of the community, which is called an endorsement—which I find absolutely insulting and I refuse to go along with. Furthermore, we are expected to cite papers, sometimes which are behind paywalls, and I think that it’s absolutely immoral to ask people to pay, outside the system, to read the papers to cite other people’s work. I could go on about the number of things that are currently wrong with the system, but instead what I would like to do is to simply, joyously reject it. I have every intention of simply sharing this with you and jealously guarding my right to shepherd this through.
00:14:06
Now, what does that mean? In two previous episodes, we’ve had interactions with academicians which I think are interesting and bear scrutiny. In the first case, in an interview with the economist Tyler Cowen, I talked to Tyler about the fact that the Boskin Commission was in fact committing economic malpractice. Now, why was that? It was because they had decided that they needed to transfer a trillion dollars over 10 years, and that they had found a devious way of doing it, which is to adjust the CPI. By backing out the amount of adjustment needed to get a trillion dollars, they decided that a 1.1% overstatement in the CPI would cause a reduction in entitlements, that is, Medicare and Medicaid payments together with Social Security, as well as an increase in taxes, because tax brackets are also indexed. Now, to my mind, it is absolutely unconscionable to say that you have a right to transfer wealth cryptically by adjusting a fundamental barometer. That would be like saying in order to meet our global warming targets, we have to recalibrate all the thermometers to show that, in fact, things have cooled. One simply can’t do that in science. But Tyler’s response, I found, was very interesting. His perspective was that this was, in fact, not a terrible thing because it was “directionally correct”. And in general, he believed that because the CPI should be considered overstated, that this was not the world’s most terrible thing to do as an economist. I respect Tyler a great deal and I enjoy his company, but I have to say that I am absolutely of a different opinion. My belief is that one has no rights and no ability as a scientist to fudge the data to meet social goals in this fashion.
00:15:57
Another interesting interaction was the interaction with Professor Agnes Callard of the University of Chicago. Now, when she listened to Episode 19 about Bret Weinstein, she found that it was a very compelling episode, but strangely, even though the point of the episode was to surface Bret’s long forgotten theory, because Bret had not been acknowledged as having predicted that laboratory mice would in particular have radically elongated telomeres where it was thought that all mice had long—radically elongated telomeres, which has incredible potential implications for drug testing and all of the work that is done on laboratory rodents as model organisms. This is an episode you should definitely listen to if you haven’t already. But Agnes’s perspective was very different than mine. Her feeling was that because we were in a situation in which the work actually surfaced, that the system worked even if it was the case that Bret’s name was erased from the history of the development, and that his theory was put in a situation in which it was not able to carry the day because, in fact, there was no record of the fact that a prediction had been made. Now, I disagreed with Agnes on that program vociferously. But what I found was that it was very telling: in general, our academic population has given up on a previous and quaint idea of decency, propriety, truth, fairness, because there simply isn’t the resource for everyone.
00:17:35
Now, I believe that current science is not necessarily unsalvageable, but it will be unsalvageable if we don’t get the very people that I rail against far more money. And I know that’s very confusing, but my belief is that the inadequate resources that we have put aside are very similar to the inadequate masks that we have put aside for our doctors. We have asked some of the world’s most gifted and smartest people to devote their lives to the study of science and technology and we have inadequately prepared them. We have put their lives and their family’s lives under incredible pressures. And what I wish to do is to, in fact, point to the very people who I have been most angry at for years, and say that part of the problem is that we need to take a hard look at how we’ve invested in science and technology and give the very people that I’m most angry at more money.
Episode Overview
00:18:26
I will explain more about this later, but I do want to give you an introduction to this episode. What I will be doing is to screen a very unusual and somewhat awkward lecture at the University of Oxford. Now, why is it so awkward? Well, first of all, I had left standard research perhaps 20 years earlier, almost. Further, I’m not a physicist, and I have only taken one or two courses in the physics major sequence. I think I’ve taken one semester of mechanics, and perhaps I took an advanced general relativity course in college. But in general, no one goes into a theoretical physics department and attempts to lecture physicists on physics. And why is that? Well, because physics is incredibly demanding, and this is almost certainly the world’s most interesting and most accomplished intellectual community. These are guys who don’t miss a trick. There are so many things to know and it is such a difficult field that it is effectively almost impossible to contribute from outside. Chemists don’t do it, and once in a blue moon, mathematicians will attempt to talk about actual, real physics. So, one thing that you’re seeing is a very unusual circumstance where somebody is trying to figure out how to give their first lecture in a physics department, and it concerns the possibility of a theory which attempts to solve the problem of “How does a fire light itself?” Another thing that you’ll see is that it’s relatively difficult to read my handwriting. I’m not gonna make any bones about it, I’ve been very vocal about having learning differences, dysgraphia, dyslexia, all sorts of different issues. Symbols come extremely difficult to me. I don’t want to spend this time making excuses. What I do want to say is the following: I will be attempting to record a short PowerPoint presentation for after the lecture to say at least what some of the constructions are more clearly.
00:20:25
This is not meant to be the actual presentation of the theory. What this is is an introduction, a down payment, and above all a historical account of what happened seven years ago at the University of Oxford when I tried to present these ideas. I’ve talked before about the twin nuclei problem and our need to get off of this planet, and if we have a hope of getting off of this planet, it really comes from fundamental physics. You see, 100 years ago, or perhaps 105, when Albert Einstein gave us general relativity, he effectively consigned us for life to the solar system. Why is that? Well, his model, his geometric model of space and time effectively creates a speed limit known as c, or the speed of light. Now, there are three rocks that are at least interesting for habitation by humans, although two of them are marginal: the Moon and Mars. One of them, of course, is unbelievable: the Earth. But I doubt that we’re going to be able to steward the Earth through our new godlike powers, which I’ve called the twin nuclei problem of cell and atom. We’ve unlocked the power of both, and I don’t think we have the wisdom to stay all in one place. So the question that I had was if there is any ability to escape to the cosmos that we can see in the night sky, where would it come from? We are almost positive that Albert Einstein’s theory of relativity is in some weird way incomplete. The Schwarzschild singularities, which give us black holes, and the initial singularities of the Robertson-Walker-Friedmann universe, which are associated with the Big Bang, are some clue that there is some subtle flaw in Einstein’s theory. So, how to go beyond Einstein? I mean, what Einstein did to Newton was to recover Newton as a special case of a more general theory that is more flexible. And in fact, this is the same problem that we have: because Albert Einstein’s theory is so fundamental, we effectively begin every theoretical physics seminar with a statement about spacetime. In other words, Albert Einstein is locked in at the ground floor. So if we can’t get below the ground floor to the foundations, it’s very difficult to make progress.
00:22:37
This is one of the things that is making it almost impossible for us to go beyond the initial revolutions of the 20th century. Do I know that this new theory, if it works, will allow us to escape? I do not. And there’s no one who can say that, and I don’t think I have the skills to develop the physical consequences of the theory, even if the theory turns out to be mostly right. What I will say is that I think that the theory is the first of its kind that I’ve seen. I believe that in part, what you will see is that, at a minimum, it is like fool’s gold. It appears to explain why we think we see three generations, but it also says that perhaps they aren’t really three generations of matter. Perhaps there are only two, even though physicists tell us that there are at least three, or perhaps more. I believe that physics tells us that the universe is chiral, that is, left-right asymmetric, but the theory is itself not chiral. Instead, it chooses to present a different idea, which is that perhaps chirality is emergent, much the way our hands are individually left-right asymmetric as our pinky is not a reflection of our thumb, but the thumb on each hand is a pairing to the other one, as is the pinky. Now, what does that mean? It means that if, perhaps, there is matter and there is force that is decoupled from our ordinary world, that that matter might restore the parity or the chirality—rather it would break the chirality and restore parity between these two halves: the matter we see, and the matter that is missing. There are a good number of other things that happen in the theory. It replaces spacetime with what I’ve termed an observerse. Now an observerse is an unusual gadget, in that it’s thought of as two separate places where physics takes place, connected by a map. That means effectively that we are in something like a stadium, where there are stands and there is a pitch, and the playing field that we think we see may not in fact be where most of the action is taking place. In fact, not all of the fields live on the same space. So when we see waves and particles dancing around, they may have separate origins in each of the two components of the observerse.
On Development and Leadership of the Theory
00:24:56
What I hope to do after this is to gracefully and gradually develop the theory under my leadership. Now, why do I say that? There is a belief in physics, and in most fields, that the field should behave in a communal fashion, and that people should put forward their ideas, and other people should joyously build upon them, and that the community should be allowed to name the various accomplishments for whoever they say accomplished those things. There’s not a way in—there’s not a way in hell that I’m letting that happen. My experience with this community is that it simply can’t be trusted to behave equitably, given the fact that it is so resource-starved and constrained. People simply do not have the freedom to be generous, kind, and accurate as to who did what.
00:25:48
Furthermore, there is an incredible premium on cherry-topping. That is, who finished something off is considered, bizarrely, much more important than who found something to begin with. Imagine you had located an island, and you named the island after the first person who could plant the flag on the top of the highest peak. This is patently offensive and ridiculous. There’s a story, years ago, about how Hilbert almost scooped Einstein by giving the Hilbert action from which Einstein’s equations could be recovered. Really? Not a chance. So if Hilbert came up with the Hilbert action and recovered Einstein’s equation, so what? I mean, the real theory actually takes place in Einstein and Grossmann, before Albert Einstein even works out a lot of the flaws in the original theory. It’s about the ideas, it’s not about the formulas, and it’s not about racing to the final form.
00:26:40
Now, I know that the community won’t agree with that, but think about this: what I’m doing is taking an incredible risk. I’m addressing you here on April Fool’s Day, and I’m saying that if there is a fool, it is certainly me, because I have sat on this theory for almost 40 years. Now, I’ve never known: Is it true? Is it false? It’s impossible to tell when you’re only talking to yourself. But in this situation, what I’ve done is I’ve taken a tremendous amount of risk, and now I’m trying to share it with you. Hopefully, I know that—well, Newton did his greatest work when he was sheltering from a great plague in England, and I would like to think that, perhaps whether or not this is correct, simply the act of somebody trying, earnestly, to share hope and some path forward would be uplifting.
00:27:33
Now, under the worst circumstances, if this doesn’t work, “What do I think?” This is a question I’m asked frequently, and there are two things that I’ll say. Many years ago, around 1987, I put forward some equations that I thought might become my thesis at the Harvard Department of Mathematics, and they were disallowed for a variety of reasons. Those equations were later discovered in, I believe, 1994, and I sat in a lecture in which I saw these equations go up on a board at the very end at MIT. And I looked at those equations and I said, “Huh, those are the exact equations I was told could never work. Why is the leading physicist in the world placing them on the board and saying that these are the equations from which all of something called Donaldson theory can be derived?” What I’m giving you, at least at a minimum, had the ability years earlier to provide those equations from a different source. There’s something called Seiberg-Witten theory, which I have no claim on. But the actual equations that are called the Seiberg-Witten equations came originally as an outgrowth from investigations of this theory. So at a bare minimum, the Seiberg-Witten revolution should have happened at Harvard rather than Princeton, and it should have been recognized that this theory was capable of at least, at a minimum, giving birth to that as a side project.
00:29:00
The other thing that I think is incredibly important is that we’ve never seen how a universe that looks like ours could possibly emerge from almost no assumptions whatsoever. And I believe that even if this theory were to turn out to be wrong, which I don’t think is likely, I believe that it would give us something to go on. We would at least have a first candidate of how a hopeful theory of everything would look and how it would go wrong. So under any circumstance, I think that I’m going to be fine if the theory doesn’t work out. I will have at least taken my shot on goal. And I think that that’s probably more than almost anyone can ask from a life, to attempt to make contact with the deepest question that we’ve ever had, which is what is this place, and what brought it into being?
00:29:50
Lastly, I want to just talk about a personal aspect of this, which is, “What does it mean to come to an end?” Whether or not this theory, in fact, does what I claim I think it does, I don’t know, but I do know that sooner or later, in the era of intercontinental land exploration, someone found the last landmass, and that must’ve been a very strange moment when there was nothing left to do. I think whether or not this theory, in fact, accomplishes that is one question, but we all have to plan for what it is that we think will happen when man, at last, learns his own source code. In fact, this was the last Edge question that I answered for John Brockman, which is, “Does something unprecedented happened when man, at last, learns his own source code?” I don’t know the answer to this, but I want to return to the same spirit that I started this [with] when I was 18 or 19, which is that of joyous investigation, of brave, open-hearted undertakings, and I also want to bring back a different style of scientific investigation. There has been far too much communalism. In fact, there is a belief that there are no lone researchers, and that everything is produced by a community. And pardon my French, but this is absolute horseshit. I’ve been so long alone with these principles, equations, and ideas that I don’t even know what my adult life will look like once I disgorge them and I begin to talk about them with the community at large. I’ve talked to many theoretical physicists who have taken some interest in them, but I’ve never put out enough to absolutely ensure that people are seeing what it is that I’m seeing. So whether or not the April Fool’s joke is on me, I cannot tell you. But I can promise you that I’m not trying to play one on you.
Acknowledgments
00:31:49
What I hope to show you is a lecture that was the first of three versions of this lecture that were delivered in Oxford over the course of a week. And, one of the things that has held me back is that I have a great number of people who I have to thank, for effectively being my Underground Railroad when my career got into serious trouble, to make sure—who made sure that I always had an opportunity to fight another day. And some of the most important of those people, one of whom occurs on this video, is Marcus du Sautoy. And Marcus, I just wanted to say thank you for your bravery, your courage, your friendship, and your encouragement. I know I’ve been absolutely impossible to you. I’ve made you wait for this, and I just want to say how much I love you.
00:32:34
I also want to thank Isadore Singer for effectively saving me from not getting a PhD by, I think, putting pressure on the Harvard department, and for coming to my assistance, making sure that I got a postdoc at MIT, despite not having any publications at all.
00:32:52
I’d like to thank Raoul Bott, who’s no longer with us, who I should have invited to my wedding. I was very angry at him, but I didn’t realize that he was saving me in a very difficult situation, against a department that probably just wanted to see me gone.
00:33:06
I’d like to thank Peter Thiel, one of my closest friends who is like a brother to me, for allowing me these seven years since this lecture to lick my wounds, to get strong, to have a 401k, to buy a house, and to begin coming back to regular society after a very difficult and strained career.
00:33:29
I’d like to thank Adil Abdulali and Michael Grossberg, the two greatest best friends from college a guy could have.
00:33:38
I’d like to thank my grandfather, Harry Rubin, who believed in things that couldn’t possibly be true and made some of them happen.
00:33:46
I’d like to thank my parents, Karen and Les Weinstein, for all the good things that they did.
00:33:50
I’d like to thank my brother Bret Weinstein and his family, Heather and the kids, for sticking by me.
00:33:55
And I’d like to thank my inlaws in Bombay, India, I hope you guys are well.
00:34:01
And lastly, I would very much like to thank my wife and my two kids, for putting up with a lot of lost weekends, a lot of lost vacations, and believing that just maybe, there was something to this, and sticking by me all of these years.
00:34:19
So, I hope everybody really enjoys this, it may not be comprehensible, and after this video finishes, I’ll do a short presentation of some of the constructions that took place—not all of the equations and things, which I think some of them were sort of botched on the board because I became disoriented the night before, and rearranged things in a way that probably wasn’t optimal. But, I’ll attempt to clarify these things going forward and to begin to present the theory, as I see whether or not I can bring myself to once again work on it somewhat close to full-time as a 54-year-old father of two. So, sit back, relax, and coming up next is the first of my three lectures at Oxford University on Geometric Unity. Be well.
Lecture at the University of Oxford

00:35:23
Marcus du Sautoy: Well, welcome to this special Simonyi lecture, and my name is Marcus du Sautoy. I’m a professor of mathematics here, and the Simonyi Professor for the Public Understanding of Science. And, Charles Simonyi prepared a manifesto when he endowed this chair, to guide the holder of the professorship in their mission, and I’d like to read one part of that manifesto to you. It said, “Scientific speculation, when so labelled, and when the concept of speculation and its place in the scientific method has been made clear to the audience, can be very exciting. It is a very effective communication tool, and it is by no means discouraged.” And it is in the spirit of this part of my mission as the Simonyi Professor that I would like to introduce today’s Simonyi special lecture.
00:36:09
I first met Eric Weinstein when we were both post-docs at the Hebrew University just over 20 years ago, and I had the feeling then that he was working on something big. But it wasn’t until two years ago that Eric met me at a bar in New York, and he began to explain the mathematics he had been working on in private for the last 20 years. As he took me through the equations he had been formulating, I began to see, emerging before my eyes, potential answers to many of the major problems in physics. It was an extremely exciting, daring proposal, and also mathematically so natural that it started to work its magic on me.
00:36:49
Over the last two years, I have had the privilege of being taken through the twists and turns of Eric’s ideas. After our post-docs in Israel, when I went the academic route, getting my professorship here in Oxford, Eric went a more independent route, working in economics, government, and finance. So he comes here today as something of an insider and an outsider, a difficult place from which to propose bold ideas. But having spent time seeing how powerful these ideas appear to be, I felt that it was time that Eric shared his ideas more widely, as I believe his perspective could give the scientific community a new story to explain to some of the big questions on the scientific books. I’m therefore very happy to provide a platform here in Oxford for Eric to share his ideas on a new theory he calls Geometric Unity. The lecture will be approximately 70 minutes after which we will have a period to ask questions. Eric.
00:37:51
Eric Weinstein: So, it’s a great pleasure to be here in Oxford. For those of you who are not aware, it is possible that no other university in the world has kept the faith for so long with Einstein’s great vision of a final theory for physics as a theory of pure geometry, a sort of elegance and simplicity of the highest order. And the names that are associated with Oxford that weigh heavy on me are [Michael] Atiyah, [Roger] Penrose, [Graeme] Segal, [Nick] Woodhouse, [Nigel] Hitchin—it’s a very long list of people who, even when fashion did not hold those ideas in favor, always kept the faith that there was much to be learned from the geometric perspective on physics.
00:38:38
Of course, unified field theory, in some sense, acquired a stigma with Einstein’s failure to find it, in the sense that even someone like Einstein, being tempted by the siren song of geometry, might lose their footing and go astray. And, in the years since, we’ve had a replacement theory, which is that what is really calling our generations is the quest to quantize general relativity and gravity. And I’d like to go back to the sort of earlier perspective, that there is no evidence to date, in my mind, that we are being called to quantize general relativity directly. In fact, there’s been more effort spent on that quest, without very tangible results, than Einstein spent as one man, searching for years, for unified field theory. So we have to, in some sense, begin to undo some of what we think we know, in order to truly reconsider and allow me to put some of these ideas before you today.
00:39:47
Marcus asked me to begin presenting these ideas here. And hopefully this is a first opportunity, but if the ideas are not good, then lighting on the aisles will lead you to safety, and your exits may be behind you. But, in the event of a good flight, hopefully this will begin a conversation rather than end one. I feel, in some sense, that I’m presenting the works of another man, a younger man, someone who came of age right in the middle of the great string theory boom with the anomaly cancellation in 1984. And I look at this work, and I see a young person struggling with the idea, ‘Why can’t I see that string theory is going to answer all of these questions over the next 10 years?’ as we were told at the time, and making a very dangerous decision, which was, ‘I think I’m not going to follow that particular path, and I’m going to follow another.’ And it’s not clear where this path is going to lead us, but we’re going to explore it today and see as best we can. So in some sense, I’ve been able to polish some of that young man’s work, but I’m also struggling to reconstruct it, because as someone spending full time on that theory, he knew a lot of things that I no longer know.
00:41:05
So, with that as a beginning, I’m just going to say one disclaimer, which is that this is not a usual talk. And whatever contract a speaker usually has with the audience, right now we’re going to break that contract. This is a talk about ideas, and some of these ideas are bold, some of them may offend some people because there’s a sense that you don’t have a right to be considering those ideas, but I go back to the admonition of Jim Watson that said if you’re going to try to make progress, big progress, you are by definition unqualified to be doing whatever it is that you’re doing. So, in that spirit, let us begin.
The Current Picture of Physics
00:41:47
What is physics to physicists today? How do they see it different from the way in which we might imagine the lay person sees physics? Ed Witten was asked this question in a talk he gave on physics and geometry many years ago, and he pointed us to three fundamental insights, which were his big three insights in physics. And they correspond to the three great equations.
If one wants to summarize our knowledge of physics in the briefest possible terms, there are three really fundamental observations: (i) Space-time is a pseudo-Riemannian manifold \(M\), endowed with a metric tensor and governed by geometrical laws. (ii) Over \(M\) is a vector bundle \(X\) with a nonabelian gauge group \(G\). (iii) Fermions are sections of \((\hat{S}{+} \otimes V_{R}) \oplus (\hat{S}{-} \otimes V_{\tilde{R}})\). \(R\) and \(\tilde{R}\) not isomorphic; their failure to be isomorphic explains why the light fermions are light and presumably has its origins in a representation difference \(\Delta\) in some underlying theory. All of this must be supplemented with the understanding that the geometrical laws obeyed by the metric tensor, the gauge fields, and the fermions are to interpreted in quantum mechanical terms.
Edward Witten, Physics and Geometry
00:42:16
So the first one is that somehow, physics takes place in an arena, and that arena is a manifold \(X\), together with some kind of semi-Riemannian metric structure: something that allows us to take length and angle, so that we can perform measurements at every point in this spacetime or higher-dimensional structure, leaving us a little bit of head room. The equation most associated with this is the Einstein field equation. And of course, I’ve run into the margin. So it says that a piece of the Riemann curvature tensor, the Ricci tensor minus an even smaller piece, the scalar curvature multiplied by the metric, is equal—plus the cosmological constant—is equal to some amount of matter and energy, the stress-energy tensor. So it’s intrinsically a curvature equation.
$$R_{\mu\nu} – \frac{1}{2}Rg_{\mu\nu} + \Lambda g_{\mu\nu} = 8 \pi T_{\mu\nu}$$
00:43:47
The second fundamental insight—I’m going to begin to start drawing pictures here as well. So, if this is the spacetime manifold, the arena; the second one concerns symmetry groups which cannot, necessarily, be deduced from any structure inside of the arena. They are additional data that come to us out of the blue without explanation. And these symmetries from a non-Abelian group, which is currently:
$$ \text{SU}(3) \text{ (color)} \times \text{SU}(2) \text{ (weak isospin)} \times \text{U}(1) \text{ (weak hypercharge)}$$
Which breaks down to \(\text{SU}(3) \times \text{U}(1)\), where the broken \(\text{U}(1)\) is the electromagnetic symmetry. This equation is also a curvature equation—the corresponding equation—and it says that this time, the curvature of an auxiliary structure known as a gauge potential, when differentiated in a particular way is equal, again, to the amount of stuff in the system that is not directly involved in the left-hand side of the equation. So it has many similarities to the above equation, both involve curvature. One involves a projection, or a series of projections. The other involves a differential operator.
$$d^*_A F_A = J(\psi)$$
00:45:44
The third point surrounds the matter in the system. And here we have a Dirac equation, again coupled to a connection. But one of the great insights is that the reason for the lightness of matter in the natural mass scale of physics has to do with the fact that this \(\psi\) really should have two components, and the differential operator should map to one component on the other side of the equation, but the mass operator should map to another. And so if one of the components is missing, if the equation is intrinsically lopsided—chiral, asymmetric—then the mass term and the differential term have difficulty interacting, which is sort of overcompensating for the mass scale of the universe, so you get to a point where you actually have to define a massless equation. But then, just like overshooting a putt, it’s easier to knock it back by putting in a Higgs field in order to generate an as-if fundamental mass through the Yukawa couplings. So matter is asymmetric, and therefore light.
$$ \unicode{x2215}\kern-0.55em \partial_A \psi = m \psi $$
00:47:35
And then, interestingly, he went on to say one more thing. He said of course, these three central observations must be supplemented with the idea that this all takes place treated in quantum mechanical fashion, or quantum field theoretic. So it’s a bit of an after-market modification rather than, in his opinion at the time, one of the core insights. I actually think that that’s, in some sense, about right. Now, one of my differences with the community, in some sense, is that I question whether the quantum is in good enough shape, that we don’t know whether we have a serious quantum mechanical problem or not. We know that we have a quantum mechanical problem, a quantum field theoretic problem, relative to the current formulations of these theories, but we know that in some other cases, the quantum becomes incredibly natural, sometimes sort of almost magically natural. And we don’t know whether the true theories that we will need to be generalizing, in some sense, have beautiful quantum mechanical treatments, whereas the effective theories that we’re dealing with now may not survive the quantization.
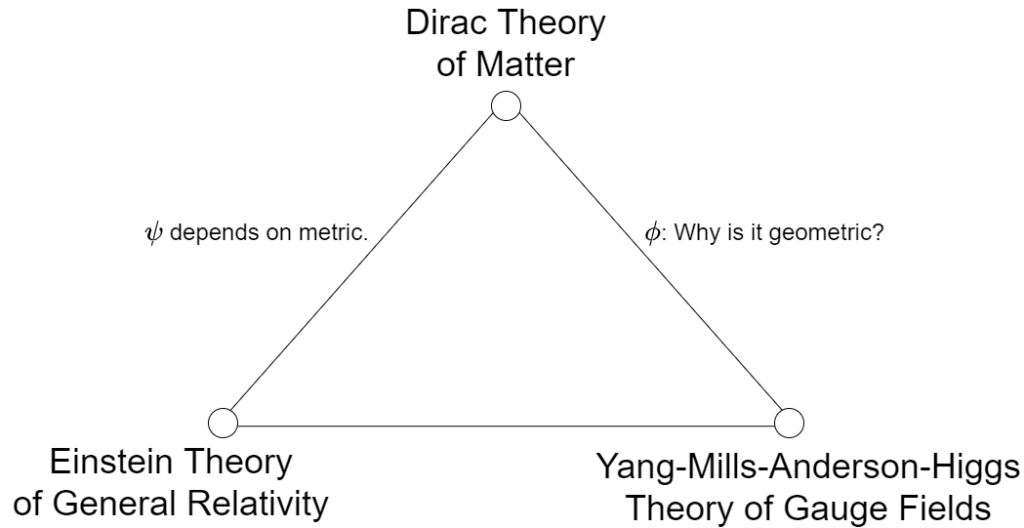
00:48:54
So what I want to do is I want to imagine a different sort of incompatibility. So let’s take our great three theories and just visually treat them as the vertices of a triangle. So I’m going to put general relativity (GR) in Einstein’s formulation, and I’m going to put the—I probably won’t write this again—Yang-Mills-Maxwell-Anderson-Higgs (YMMAH) theory over here, and I’m going to write the Dirac theory. What I want to explore is the incompatibilities, not at the quantum level, but the geometric input. All three of these are geometric theories. And the question is, what are the compatibilities or incompatibilities at the level of geometry—before the theory is treated quantum mechanically?
00:50:01
Well, in the case of Einstein’s general relativity, we can rewrite the Einstein theory by saying that there’s a projection map due to Einstein of a curvature tensor, where I’m going to write that curvature tensor as I would in the Yang-Mills theory. That should be an LC for Levi-Civita. So, the Einstein projection of the curvature tensor of the Levi-Civita connection of the metric on this side, and on this side, I’m going to write down this differential operator, the adjoint of the exterior derivative coupled to a connection. And you begin to see that we’re missing an opportunity, potentially. What if the \(F_A\)s were the same in both contexts? Then you’re applying two separate operators, one zeroth-order and destructive, in the sense that it doesn’t see the entire curvature tensor; the other inclusive, but of first-order. And so the question is, is there any opportunity to do anything that combines these two?
$$ P_E(F_{\nabla^{LC}h}) \neq h^{-1}P_E(F_{\nabla^{LC}}) h $$
00:51:15
But the problem is that the hallmark of the Yang-Mills theory is the freedom to choose the data, the internal quantum numbers that give all the particles their personalities beyond the mass and the spin. In addition to all of that freedom is some means of taking away some of the redundancy that comes with that freedom, which is the action of the gauge group. Now we can allow the gauge group of symmetries to act on both sides of the equation, but the key problem is that if I act on connections on the right and then take the Einstein projection, this is not equal to first taking the projection and then conjugating with the gauge action. So the problem is that the projection is based on the fact that you have a relationship between the intrinsic geometry—if this is an ad-valued 2-form—the 2-form portion of this and the adjoint portion of this are both associated to the structure group of the tangent bundle. But the gauge rotation is only acting on one of the two factors, yet the projection is making use of both of them. So there is a fundamental incompatibility, and the claim that Einstein’s theory is a gauge theory relies more on analogy than on an exact mapping between the two theories.
00:53:11
What about the incompatibilities between the Einstein theory of general relativity and the Dirac theory of matter? I was very struck that, if we’re going to try to quantize gravity and we associate gravity with the spin-2 field \(g_{\mu \nu}\), we actually have a pretty serious problem, which is if you think about spinors, electrons, quarks, as being waves in a medium, and you think about photons as being waves in a different medium, [the] photon’s medium does not depend on the existence of a metric. One-forms are defined whether or not a metric is present yet spinors are not. So if we’re going to take the spin-2 \(g_{\mu \nu}\) field to be quantum mechanical, if it blinks out and does whatever the quantum does between observations, in the case of the photon, it is saying that the waves may blink out, but the ocean need not blink out. In the case of the Dirac theory, it is the ocean, the medium, in which the waves live that becomes uncertain itself. So even if you’re comfortable with the quantum, to me, this becomes a bridge too far. So the question is how do we liberate the definition? How do we get the metric out from its responsibilities? It’s been assigned far too many responsibilities. It is responsible for a volume form, for differential operators, it’s responsible for measurement, it’s responsible for being a dynamical field, part of the field content of the system.
00:55:06
Lastly, we have the compatibilities and incompatibilities between Yang-Mills and in the Dirac theory. These may be the most mild of the various incompatibilities, but it is an incompatibility of naturality. Where the Dirac field, Einstein’s field, and the connection fields are all geometrically well-motivated, we push a lot of the artificiality that we do not understand into the potential for the scalar field that gives everything its mass, so we tend to treat it as something of a mysterious fudge factor. So the question is if we have a Higgs field, why is it here and why is it geometric? It has long been the most artificial sector of our models.
00:55:59
The proposal that I want to put to you today is that one of the reasons that we may be having trouble with unification is that the duty, our duty, may be to generalize all three vertices before we can make progress. That’s daunting because in each case, it would appear that we can make an argument that this, that, and the other vertex are the simplest possible theories that could live at that vertex. We know, for example, the Dirac operator is the most fundamental of all the elliptic operators in Euclidean signature, generating all of the Atiyah-Singer theory. We know that Einstein’s theory is, in some sense, a unique spin-2 massless field capable of communicating gravity, which can be arrived at from field-theoretic rather than geometric considerations. In the Yang-Mills case, it can be argued that the Yang-Mills theory is the simplest theory that can possibly result. Where we’re taking the simplest Lagrangian in the Einstein case, looking only at the scalar curvature, in the Yang-Mills case, we have no substructure, and so we’re doing the most simple-minded thing we can do by taking the norm-square of the curvature and saying whatever the field strength is, let’s measure that size. So if each one of these is simplest possible, doesn’t Occam’s razor tell us that if we wish to remain in geometric field theory, that we’ve already reached bottom, and that what we’re being asked to do is to abandon this as merely an effective theory? That’s possible. And I would say that that, in some sense, represents a lot of conventional wisdom. But there are other possibilities.

00:57:41
There are other possibilities that while each of these may be simplest in its category, they are not simplest in their interaction. For example, we know that Dirac famously took the square root of the Klein-Gordon equation to achieve the Dirac equation—he actually took two square roots, one of the differential operator, and another of the algebra on which it acts. But could we not do the same thing by re-interpreting what we saw in Donaldson theory and Chern-Simons theory, and finding that there are first-order equations that imply second-order equations that are nonlinear and in the curvature? So let’s imagine the following: we replace the Standard Model with a true second-order theory. We imagine that general relativity is replaced by a true first-order theory. And then we find that the true second-order theory admits of a square root and can be linked with the true first-order theory. This would be a program for some kind of unification of Dirac’s type, but in the force sector. The question is, “Does this really make any sense? Are there any possibilities to do any such thing?”
Motivations for Geometric Unity
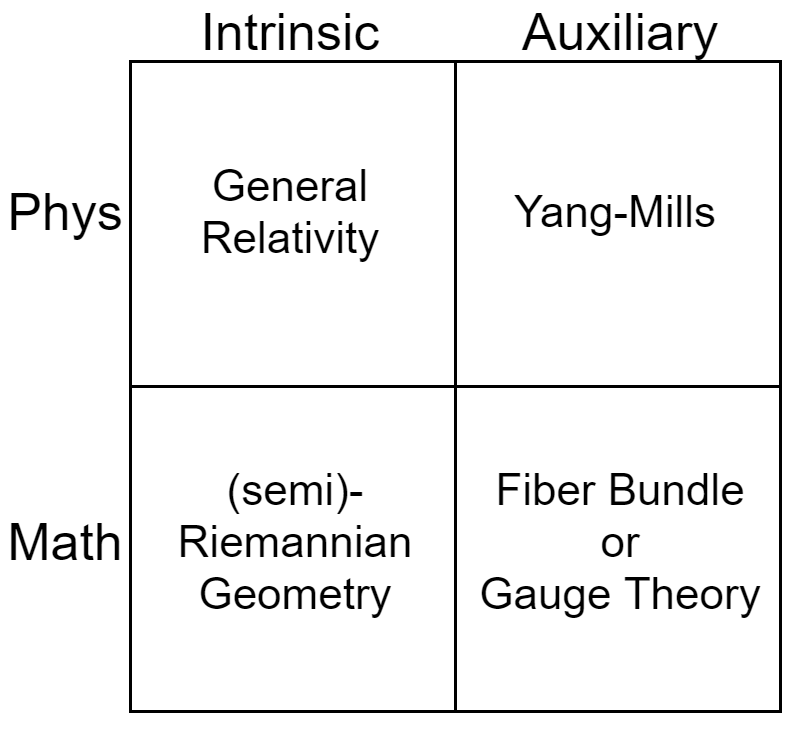
00:59:12
So what I’d like to do is I’d like to talk a little bit about what the Geometric Unity (GU) proposal is. So we have a division into intrinsic theories and auxiliary theories, between physics and mathematics, more specifically geometry. An intrinsic physical theory would be general relativity. An auxiliary physical theory would be the Yang-Mills theory with the freedom to choose internal quantum numbers. At the mathematical level, an intrinsic theory would be—let’s be a little fastidious—the older semi-Riemannian geometry: the study of manifolds with length and angle. But auxiliary geometry is really what’s taken off of late since the revolution partially begun at Oxford when Is Singer brought insights from Stony Brook to the UK. And so we’re going to call this fiber bundle theory, or modern gauge theory.
01:00:48
Geometric Unity is the search for some way to break down the walls between these four boxes. What’s natural to one theory is unnatural to another. Semi-Riemannian geometry is dominated by these projection operators as well as the ability to use the Levi-Civita connection. Now, some aspects of this are less explored. Torsion tensors are definable in semi-Riemannian geometry, but they are not used to the extent that you might imagine. In the case of fiber bundle theory, the discovery of physicists that the gauge group was fantastically important came as something of a shock to the mathematicians who had missed that structure, and have since exploited it to great effect. So what we’d like to do is we’d like to come up with some theory that is intrinsic, but allows us to play some of the games that exist in other boxes. How can we try to have our cake, eat it, and use the full suite of techniques that are available to us? So, our perspective is that it is the quantum that may be the comparatively easy part, and that the unification of the geometry, which has not occurred, may be what we’re being asked to do. So let’s try to figure out, what would a final theory even look like?
01:02:12
When I was a bit younger, I remember reading this question of Einstein, in which he said I’m not really interested in some of the details of physics. What really concerns me is whether the creator had any choice in how the world was constructed. And some people may have read that as a philosophical statement, but I took that as an actual call for a research program. So I’d like to describe that research program and try to unpack what I think he was saying.
01:02:46
We talk a lot about unification, but we hardly ever actually imagine if we had a unified theory, what would it look like? Let us imagine that we cannot figure out the puzzle of why is there something rather than nothing. But if we do have a something, that that something has as little structure as possible, but it still invites us to work mathematically. So to me, the two great theories that we have mathematically and in physics are calculus and linear algebra. If we have calculus and linear algebra, I’m going to imagine that we have some manifold, at least one of dimension four—but it’s not a spacetime. It doesn’t have a metric. It’s not broken down into two different kinds of coordinates, which then have some bleed into each other, but still maintains a distinction. It’s just some sort of flabby proto-spacetime, and in the end it has got to fill up with stuff and give us some kind of an equation. So let me write an equation.
$$\delta^\omega(\mathscr{D}^\omega_2 \mathscr{D}^\omega_1) = 0$$
01:04:13
So I have in mind differential operators, parameterized by some fields \(\omega\), which when composed are not of second-order if these are first-order operators, but of zeroth-order, and some sort of further differential operator saying that whatever those two operators are in composition is in some sense harmonic. Is such a program even possible? So if the universe is in fact capable of being the fire that lights itself, is it capable of managing its own flame as well and closing up? What I’d like to do is to set ourselves an almost impossible task, which is to begin with this little data in a sandbox, to use a computer science concept.
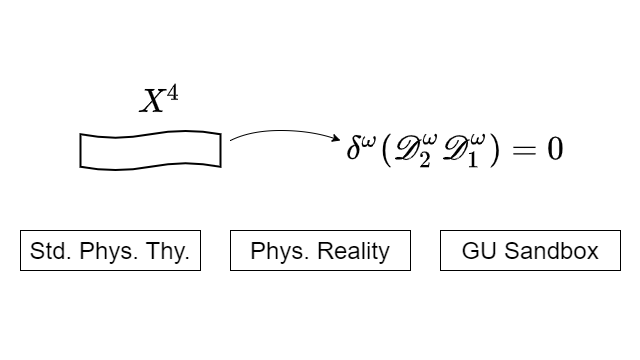
01:05:11
So, if here is physical reality, standard physics is over here, we’re going to start with the sandbox, and all we’re going to put in it is \(X^4\). And we’re going to set ourselves a strait-jacketed task of seeing how close we can come to dragging out a model that looks like the natural world that follows this trajectory. While it may appear that that is not a particularly smart thing to do, I would like to think that we could agree that it is quite possible that if that were to be the case, we might say that this is what Einstein meant by a creator, which was his anthropomorphic concept for necessity and elegance and design, having no choice in the making of the world.
The Observerse and Four Versions of GU
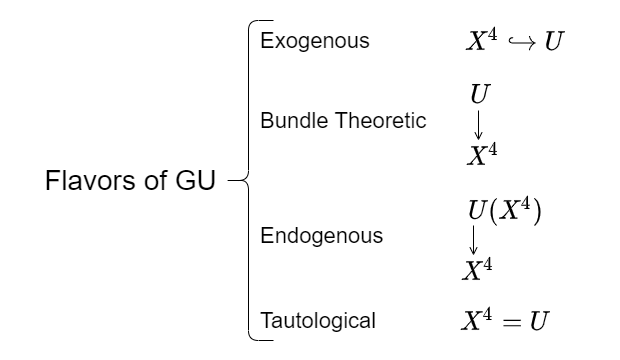
01:06:19
So with that, let us begin to think about what we mean today by Geometric Unity. GU comes in four flavors, but I’m only getting one shot to do this, so I’m going to do the most exciting of them to me.
01:06:42
There’s a completely exogenous flavor. And what I’m gonna do is I’m going to take the concept of observation and I’m going to break the world into two pieces: a place where we do our observation and a place where most of the activity takes place. And I’m going to try and do this without loss of generality. So in this case, we have \(X^4\) and it can map into some other space, and we are going to call this an observerse. The idea of an observerse is a bit like a stadium: you have a playing field and you have stands. They aren’t distinct entities, they’re coupled. And so fundamentally, we’re going to replace one space with two. Exogenous model simply means that \(U\) is unrestricted, although larger than \(X^4\), so any manifold of four dimensions or higher that is capable of admitting \(X^4\) as an immersion.
01:07:41
The next model we have is the bundle theoretic, in which case, \(U\) sits over \(X\) as a fiber bundle.
01:07:58
The most exciting, which is the one we’ll deal with today, is the endogenous model, where \(X^4\) actually grows the space \(U\) where the activity takes place. So we talk about extra dimensions, but these are, in some sense, not extra dimensions. They are implicit dimensions within \(X^4\).
01:08:17
And last, to proceed without loss of generality, we have the tautological model. In that case, \(X^4 = U\), and the immersion is the identity, and without loss of generality, we simply play our games on one space. Okay?
Rules for Constructing GU
01:08:36
Now, we need rules. The rules are… sorry, feedback. No choice of fundamental metric. So we imagine that Einstein was presented with a fork in the road, and it’s always disturbing not to follow Einstein’s path, but we’re in fact going to turn Einstein’s game on its head and see if we can get anywhere with that, right? It’s also a possibility that because Einstein’s theory is so perfect, that if there’s anything wrong with it, it’s very hard to unthink it because everything is built on top of it.
01:09:13
So let’s make no choice of fundamental metric, and in fact, let’s go more ambitious, and let’s say we’re going to reverse the logic of Einstein. In Einstein, the metric is fundamental, but the Levi-Civita connection from which we deduce the curvature is emergent, right? So the fundamental theorem of Riemannian geometry is that every metric causes a connection to emerge, and then the curvature is built on the connection. We turn this around. We imagine we’re looking for a connection, and we wish it to build a metric, because connections are amenable to quantization in a way that metrics are not.
01:09:47
The next point is that we always want to have a plan to return to finite dimensions without losing sight of the quantum.
01:09:56
And lastly, we want to liberate matter from its dependence on the metric for its very existence. So we now need to build fermions onto our four-dimensional manifold in some way without ever choosing a metric, if we’re even going to have any hope of playing a game involving matter, starting from this perspective of no information other than the most bare information. Let’s get started.
Constructing Endogenous GU: Choosing All Metrics
01:10:24
We take \(X^4\). We need metrics, we have none. We’re not allowed to choose one, so we do the standard trick: we choose them all.
$$U^{14} = \text{met}(X^4)$$
01:10:36
So we allow \(U^{14}\) to equal the space of metrics on \(X^4\) pointwise. Therefore, if we propagate on top of this—let me call this (\(\pi\)) the projection operator. If we propagate on \(U^{14}\), we are, in some sense, following a Feynman-like idea of propagating over the space of all metrics, but not at a field level, at a pointwise tensorial level.
01:11:03
Is there a metric on \(U^{14}\)? Well, we both want one and don’t want one. If we had a metric from the space of all metrics, we could define fermions, but we would also lock out any ability to do dynamics. We want some choice over what this metric is, but we don’t want full choice, because we want enough to be able to define the matter fields to begin with.
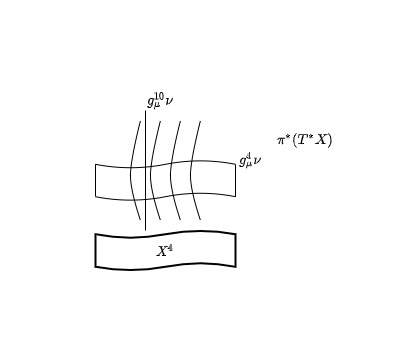
01:11:22
It turns out that if this is \(X^4\), and this is this particular endogenous choice of \(U^{14}\), we have a 10-dimensional metric along the fibers. So we have a \(g^{10}_{\mu \nu}\). Further, for every point in the fibers, we get a metric downstairs on the base space. So if we pull back the cotangent bundle, we get a metric \(g^4_{\mu \nu}\) on \(\pi*\) of the cotangent bundle of \(X\).
Chimeric Bundle
01:12:17
We now define the chimeric bundle, right? And the chimeric bundle is this direct sum of the vertical tangent bundle along the fibers with the pullback, which we’re going to call the horizontal bundle, from the base space. So the chimeric bundle is going to be the vertical tangent space of 10 dimensions to \(U\), direct sum the cotangent space, which we’re going to call horizontal, to \(U\). And the great thing about the chimeric bundle is that it has an a priori metric. It’s got a metric on the 4, a metric on the 10, and we can always decide that the two of them are naturally perpendicular to each other.
$$ T_V^{10}(U) \oplus T_H^{4*}(U) $$
01:13:00
Furthermore, it is almost canonically isomorphic to the tangent bundle or the cotangent bundle, because we either have 4 out of 14, or 10 out of 14 dimensions, on the nose. So the question is, what are we missing? And the answer is that we’re missing exactly the data of a connection. So this bundle, chimeric \(C\)—we have \(C\) is equal to the tangent bundle of \(U\) up to a choice of a connection \(\theta\).
$$ CU \overset{\theta}{=} TU $$
01:13:32
And this is exactly what we wanted. We have a situation where we have some field on the manifold \(X\) in the form of a connection, which is amenable, more friendly to quantization, which is now determining a metric, turning around the Levi-Civita game. And the only problem is that we’ve had to buy ourselves into a different space than the one we thought we wanted to work on.
01:13:55
But now, as \(\theta\) changes, the fermions are defined on the chimeric bundle, and it’s the isomorphism from the chimeric bundle to the tangent bundle of the space \(U\), which is variant—which means that the fermions no longer depend on the metric. They no longer depend on the \(\theta\) connection. They are there if things go quantum mechanical, and we’ve achieved our objective of putting the matter fields and the spin-1 fields on something of the same footing.
Observerse Conclusion
01:14:27
But, and I want to emphasize this: one thing most of us—we think a lot about final theories and about unification, but until you actually start daring to try to do it, you don’t realize what the process of it feels like. And, try to imagine conducting your life where you have no children, let’s say, and no philanthropic urges, and what you want to do is you want to use all of your money for yourself and die penniless, right? Like a perfect finish. Assuming that that’s what you wanted to do, it would be pretty nerve-wracking at the end, right? How many days left do I have? How many dollars left do I have? This is the process of unification in physics. You start giving away all of your most valuable possessions, and you don’t know whether you’ve given them away too early, whether you husbanded them too long, and so in this process, what we’ve just done is we’ve started to paint ourselves into a corner. We got something we wanted, but we’ve given away freedom. We’re now dealing with a 14-dimensional world.
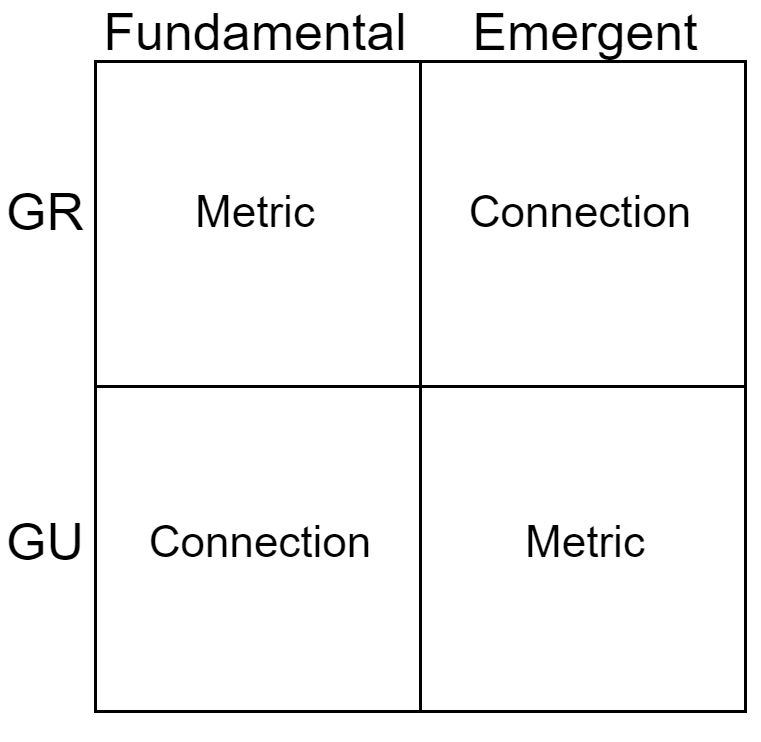
01:15:39
Well, let me just sum this up by saying: between fundamental and emergent, Standard Model and GR… Let’s do GR. Fundamental is the metric, emergent is the connection. Here in GU, it is the connection that’s fundamental and the metric that’s emergent.
Unified Field Content
01:16:23
In the next unit of GU—so this is sort of the first unit of GU. Are there any quick questions having to do with confusion, or may I proceed to the next unit?

01:16:36
Okay. The next unit of GU is the unified field content. What does it mean for our fields to become unified? There are, in fact, only—at this moment—two fields that know about \(X\). \(\theta\), which is the connection that we’ve just talked about, and a section \(\sigma\), that takes us back so that we can communicate back and forth between \(U\) and \(X\). We now need field content that only knows about \(U\), which now has a metric depending on \(\theta\).
The Trade
01:17:32
A particular member of the audience is a hedge fund manager who taught me that there is something of a universal trade. And a universal trade has four components:
- You have to have a view.
- You have to have a trade expression.
- You have to be able to calculate your cost of carry.
- You need a catalyst.
Our view is going to be that somebody doesn’t understand what trade is possible and we’re going to make a trade that looks like one of the worst trades of all time, and hopefully, if we have enough conviction, we’re going to have a catalyst to show that we actually got the better part of the deal. What is that trade? What is it that we think has been blocking progress?
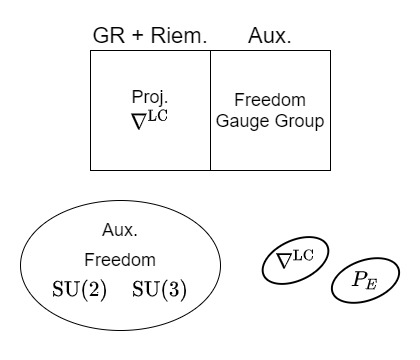
01:18:16
In GR and Riemannian geometry, as we’ve said, we have the projection operators and we also have the Levi-Civita connection. In the auxiliary theory, we have freedom to choose our field content, and we have the ability to get rid of much excess through the symmetries of the gauge group. We’re going to take particle theory, and we’re going to make a bad trade, or what appears to be a bad trade, which is that we are going to give away the freedom to choose our field content, which is already extremely, as I think I said in the abstract, baroque, with all of the different particle properties. And we’re going to lose the ability to use the gauge group, because we’re going to trade it all.
01:19:27
You have the family cow and you have some magic beans.
01:19:40
So it’s now time to trade the family cow for the magic beans and bring them home, and see whether or not we got the better of the deal.
01:20:01
Okay. What is it that we get for the Levi-Civita connection? Well, not much. One thing we get is that normally, the space of connections is an affine space: not a vector space, but an affine space—almost a vector space, a vector space up to a choice of origin. But with the Levi-Civita connection, rather than having an infinite plane, with an ability to take differences but no real ability to have a group structure, you pick out one point, which then becomes the origin. That means that any connection \(A\) has a torsion tensor \(T_A\), which is equal to the connection minus the Levi-Civita connection. So we get a tensor that we don’t usually have. Gauge potentials are not usually well-defined, they’re are only defined up to a choice of gauge.
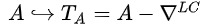
01:21:00
So that’s one of the things we get for our Levi-Civita connection, but because the gauge group is going to go missing, this has terrible properties with respect to the gauge group. It almost looks like a representation. But in fact, if we let the gauge group act, there’s going to be an affine shift.
01:21:21
Furthermore, as we’ve said before, the ability to use projection operators, together with the gauge group, is frustrated by virtue of the fact that these two things do not commute with each other. So now the question is, how are we going to prove that we’re actually making a good trade?
01:21:48
[The] first thing we need to do is we still have the right to choose intrinsic field content. We have an intrinsic field theory, so if you consider the structure bundle of the spinors—we’ve built the chimeric bundle, so we can define Dirac spinors on the chimeric bundle. If we’re in Euclidean signature, a 14-dimensional manifold has Dirac spinors of dimension two to the dimension of the space divided by two. Right? So \(2^{14}\) over \(2^7\) is \(128\).
$$ C ⇝ \unicode{x2215}\kern-0.55em S(C) $$
$$ P_{U(\unicode{x2215}\kern-0.4em S)} = P_{U(128)} $$
01:22:24
So we have a map into a structure group of \(U(128)\), at least in Euclidean signature—we can get to mixed signatures later. From that, we can form the associated bundle.
$$ P_{U(\unicode{x2215}\kern-0.4em S)} \times _{\text{Ad}}U(\unicode{x2215}\kern-0.55em S) $$
01:22:54
And sections of this bundle are either, depending upon how you want to think about it, the gauge group \(\mathcal{H}\), or \(\Xi\), a space of \(\sigma\) fields—nonlinear.
$$ \Gamma^\infty(P_{U(\unicode{x2215}\kern-0.4em S)} \times _{\text{Ad}}U(\unicode{x2215}\kern-0.55em S)) = \begin{cases} \mathcal{H} \text{ gauge group}\\
\Xi \text{ sigma fields (non-linear)} \end{cases} $$
01:23:25
There’s no reason that we can’t choose this as field content. Again, we’re being led by the nose like a bull. If we want to make use of the symmetries of the theory, we have to promote some symmetry to being part of the theory, and we have to let it be subjected to dynamical laws. We’re going to lose control over it. But we’re not dead yet, right? We’re fighting for our life to make sure that this trade has some hope. So potentially, by including symmetries as field content, we will have some opportunity to make use of the projections. So for those of you who…
Inhomogeneous Gauge Group and Tilted Gauge Group
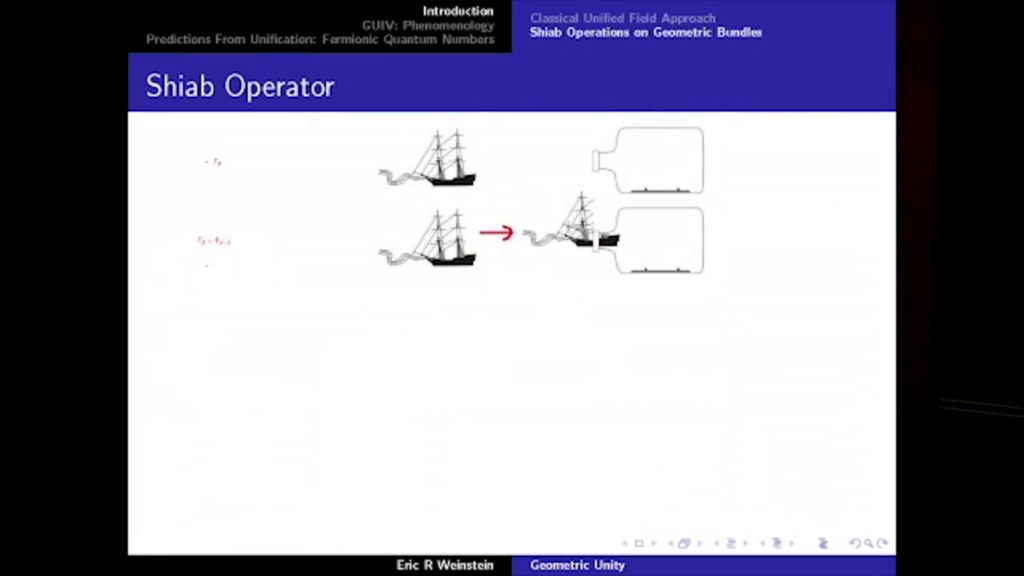
01:24:06
So when I was thinking about this, I used to be amazed by ships in bottles, and I must confess that I never figured out what the trick was for ships in bottles. But once I saw it, I remembered thinking, ‘That’s really clever.’ So, if you’ve never seen it, you have a ship, which is like a curvature tensor, and imagine that the mast is the Ricci curvature. If you just try to shove it into the bottle, you’re undoubtedly going to snap the mast. So, you imagine that you’ve transformed your gauge fields, you’ve kept track of where the Ricci curvature was, you try to push it from one space, like ad-valued 2-forms, into another space, like ad-valued 1-forms, where connections live.
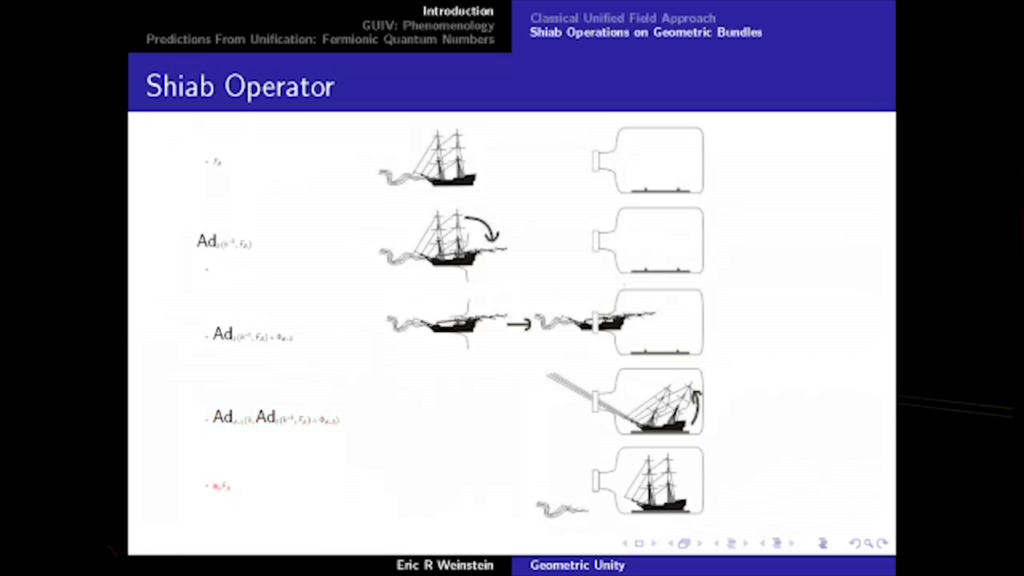
01:24:54
That’s not a good idea. Instead, what we do is the following: imagine that you’re carrying around group theoretic information, and what you do is you do a transformation based on the group theory. So you lower the mast, you push it through the neck, having some string attached to the mast, and then you undo the transformation on the other side.
01:25:18
This is exactly what we’re going to hope is going to save us in this bad trade that we’ve made. Because we’re going to add field content that has the ability to lower the mast and bring the mast back up, we’re going to hope to have a theory which is going to create a commutative situation. But then, once we’ve had this idea, we start to get a little bolder.
01:25:43
Let’s think about unified content. We know that we want a space of connections \(\mathscr{A}\) for our field theory. But we know, because we have a Levi-Civita connection, that this is going to be equal on the nose to ad-valued 1-forms as a vector space. The gauge group represents on ad-valued 1-forms.
$$ \mathscr{A} = \Omega^1(ad) $$
01:26:08
So, if we also have the gauge group, but we think of that instead as a space of \(\sigma\) fields, what if we take the semi-direct product at a group theoretic level between the two and call this our group of interest?
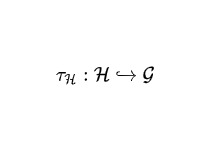
01:26:25
Well by analogy, we’ve always had a problem with the Poincaré group being too intrinsically tied to rigid, flat Minkowski space. What if we wanted to do quantum field theory in some situation which was more amenable to a curved space situation? It’s possible that we should be basing it around something more akin to the gauge group. And in this case, we’re mimicking the construction, where \(\Xi\) here would be analogous to the Lorentz group fixing a point in Minkowski space, and ad-valued 1-forms would be analogous to the four momentums we take in the semi-direct product to create the inhomogeneous Lorentz group, otherwise known as the Poincaré group, or rather its double cover to allow spin.
01:27:12
So we’re going to call this the inhomogeneous gauge group, or iggy. And this is going to be a really interesting space, because it has a couple of properties. One is it has a very interesting subgroup. Now, of course, \(\mathcal{H}\) includes into \(\mathcal{G}\) by just including onto the first factor, but in fact, there’s a more interesting homomorphism brought to you by the Levi-Civita connection. So, this magic bean trade is going to start to enter more and more into our consciousness.
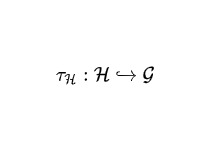
01:27:54
If I take an element \(h\), and I map that in the obvious way into the first factor, but I map it onto the Maurer-Cartan form—I think that’s when I wish I remembered more of this stuff—into the second factor, it turns out that this is actually a group homomorphism.
$$ h \rightarrow (h, h^{-1} d_{A_0} h) $$
01:28:25
And so we have a nontrivial embedding, which is in some sense diagonal between the two factors. That subgroup we are going to refer to as the tilted gauge group, and now our field content, at least in the bosonic sector, is going to be a group manifold, an infinite-dimensional function space Lie group, but a group nonetheless. And we can now look at \(\mathcal{G} / \mathcal{H}_\tau\), and if we have any interesting representation of \(\mathcal{H}\), we can form homogeneous vector bundles and work with induced representations. And that’s what the fermions are going to be. So the fermions in our theory are going to be \(\mathcal{H}\) modules, and the idea is that we’re going to work with vector bundles of the form inhomogeneous gauge group producted over the tilted gauge group.
$$ \mathcal{G} / \mathcal{H_{\tau}} $$
$$ \mathcal{E} = \mathcal{G} \times_{H_{\tau}} \Upsilon $$
$$ \Upsilon_H = \text{Fermion Cover} $$
01:29:47
Now, just as in the finite dimensional case, we have a linear and a nonlinear component, right? Because at the topological level, this is just a Cartesian product. So if we wished to take products of fermions, of spinorial fields, we have a place to accept them. We can’t figure out necessarily how to map them into the nonlinear sector, but we don’t want to. So just the way when we look at supersymmetry, we can take products of the spin-1/2 fields and map them into the linear sector, we can do the same thing here.
01:30:19
So, what we’re talking about is something like a supersymmetric extension of the inhomogeneous gauge group analogous to supersymmetric extensions of the double cover of the inhomogeneous Lorentz or Poincaré group. Further, because this construction is at the level of groups, we’ve left a slot on the left-hand side on which to act. So, for example, if we want to take regular representations on the group, we can act by the group \(\mathcal{G}\) on the left-hand side, because we’re allowing the tilted gauge group to act on the right-hand side. So it’s perfectly built for representation theory, and if you think back to Wigner’s classification, and the concept that a particle should correspond to an irreducible representation of the inhomogeneous Lorentz group, we may be able to play the same games here, up to the issue of infinite-dimensionality.
01:31:15
So right now, our field content is looking pretty good. It’s looking unified, in the sense that it has an algebraic structure that is not usually enjoyed by field content, and the field content from different sectors can interact and know about each other, provided we can drag something out of this with meaning.
Toolkit for the Unified Field Content
01:31:38
Now, what would it mean to be able to use a gauge group in an intrinsic theory like this? We would be talking about something like an action, let’s say a first-order action. And it would take the group \(\mathcal{G}\), let’s say to the real numbers, invariant, not under the full group, but under the tilted gauge subgroup.
$$ S_1:\mathcal{G} \rightarrow \mathbb{R} $$
$$ \text{Invariant } \mathcal{H}_\tau $$
01:32:13
And now the question is, do we have any such actions that are particularly nice, and could we recognize them the way Einstein did, by trying to write down not the action—and Hilbert was the first one to write that down but I, you know, I always feel defensive, because I think Einstein and Grossmann did so much more to begin the theory, and that the Lagrangian that got written down was really just an inevitability. So, just humor me for this talk, and let me call it the Einstein-Grossmann Lagrangian. Hilbert’s certainly done fantastic things and has a lot of credit elsewhere, and he did do it first. But here, what we had was that Einstein thought in terms of the differential of the action, not the action itself. So, what we’re looking for is equations of motion or some field \(\alpha\), where \(\alpha\) belongs to the 1-forms on the group.
$$ \alpha \in \Omega^1(\mathcal{G}) $$
$$ dS_1 = \alpha = 0 $$
01:33:22
Now in this section of GU, unified field content is only one part of it. But what we really want is unified field content plus a toolkit. So we’ve restricted ourselves to one gauge group, this big unitary group on the spinors using whatever sort of inner product naturally exists on the spinors. And not spinors valued in an auxiliary structure, but intrinsic spinors.
01:34:00
The toolkit that we have is that the adjoint bundle looks like the Clifford algebra at the level of vector spaces, which is just looking like the exterior algebra on the chimeric bundle.
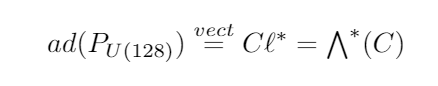
01:34:34
That means that it’s graded by degrees. [The] chimeric bundle has dimension 14, so there’s a zero-part, a one-part, a two-part, all the way up to 14. Plus, we have forms in the manifold. And so the question is, if I want to look at \(\Omega^i\) valued in the adjoint bundle, there’s going to be some element \(\Phi_i\), which is pure trace.
$$ \Omega^i(ad) \ni \Phi_i $$
01:35:12
Right? Because it’s the same representations appearing where in the usually auxiliary directions, as well as the geometric directions. So we get an entire suite of invariance, together with trivially associated invariants that come from using the Hodge star operator on the forms. I’m just going to call them, for completeness, \(\tilde{\Phi}_i\). I’m not going to deal with them.
Ship in a Bottle (Shiab) Operator
01:35:41
Now, this is a tremendous amount of freedom that we’ve just gained. Normally, we keep losing freedom, but this is the first time we actually begin to see that we have a lot of freedom, and we’re going to actually retain some of this freedom through to the end of the talk. But the idea being that I can now start to define operators which correspond to the “Ship in the Bottle” problem. I can take field content \(\varepsilon\) and \(\pi\), where these are elements of the inhomogeneous gauge group. In other words, \(\varepsilon\) is a gauge transformation, and \(\pi\) is a gauge potential.
$$ (\varepsilon, \pi) \in \mathcal{G} $$
01:36:27
And I can start to define operators:
$$ \bigcirc\kern-1.00em\circ\kern-0.62em·\text{}\kern0.3em_\varepsilon \eta = [\text{Ad}(\varepsilon^{-1}, \Phi), \eta] $$
01:36:44
So in this case, if I have a \(\Phi\), which is one of these invariants, in the form piece I can either take a contraction or I can take a wedge product. In the Lie algebra piece, I can either take a Lie product, or because I’m looking at the unitary group there’s a second possibility, which is I can multiply everything by \(i\) and go from skew-Hermitian to Hermitian and take a Jordan product using anti-commutators rather than commutators. So I actually have a fair amount of freedom, and I’m going to use a “magic bracket” notation, which in whatever situation I’m looking for, [the operator] knows what it wants to be. Does it want to do contraction? Does want to do wedge product, Lie product, Jordan product? But the point is, I now have a suite of ways of moving forms around.
01:37:34
So for example, I can define a shiab operator (ship in a bottle operator) that takes \(i\)-forms valued in the adjoint bundle to much higher-degree forms valued in the adjoint bundle.
$$ \bigcirc\kern-1.00em\circ\kern-0.62em·\text{}\kern0.3em_\varepsilon \Omega^i(ad) \rightarrow \Omega^{d-3+i}(ad) $$
01:38:00
So for this case, for example, it would take a 2-form to a \((d – 3 + 2)\) or a \((d – 1)\)-form. So curvature is an ad-valued 2-form. And, if I had such a shiab operator, it would take ad-valued 2-forms to ad-valued \((d – 1)\)-forms, which is exactly the right space to be an \(\alpha\) coming from the derivative of an action.
01:38:38
This is exactly what Einstein was doing. He took the curvature which was large, and he bent it back and he sheared off the Weyl curvature, and then he took that part and he pushed it back along the space of metrics to give us something which we nowadays call Ricci flow, an ability for the curvature to direct us to the next structure. Well, we’re doing the same thing here. We’re taking the curvature and we can now push it back onto the space of connections.
01:39:28
Audience Member: Can you just clarify what the index on the shiab is? So you take \(i\)-forms to \(d – 3 + 1\)?
01:39:38
Eric Weinstein: \(3 + i\).
01:39:43
So in this case, the idea is that we’ve actually got something for our magic beans. We have an ability, now, to get equations of motion which go along the group, in some sense—it’s as if it was a gradient vector field, except we’re using forms rather than vectors. But now what are the transformation properties?
01:40:08
Well, because the curvature… so, you have shiab—because the curvature of a connection hit by a gauge transformation is equal on the nose to the adjoint action on the Lie algebra of the curvature, we know that if we have two possible actions of conjugation under a bracket, and the bracket respects the action of the gauge group, we know that this is going to be well-preserved. In other words, we’re going to get a form that is gauge invariant relative to the tilted gauge group.
$$ F_Ah = h^{-1}(F_A)h $$
01:41:08
And so as a result, we now have the possibility for equations of motion which are well-defined, even though they involve projection operators because we’ve built the symmetries into the theory and we’re working on a group manifold to begin with.
01:41:26
What about the torsion? Can we rescue the torsion? Here, again, we have good news. The torsion is problematic, but if I look at a different field—which I’m going to call the augmented torsion, and I define it to be the regular torsion, which would be \(\Pi\) minus this expression, this turns out to be beautifully invariant again.
$$ T_{\varepsilon, \pi} = \Pi – h^{-1}d_{A_0}h $$
01:41:58
So, neither this term nor this term is gauge invariant, but they fail to be gauge invariant in exactly the same way. So, an important principle of life which I took too long to realize is that if you have one disease, you’re in real trouble. But if you have two diseases, you always have the possibility of having one disease kill the other disease. This is true in renormalization theory, it’s true in Black-Scholes theory, it’s true all over the place. So what we have here is we’ve gotten more diseases into the theory, but an even number of diseases allow us to have no disease at all. So now we have two great tensors: we’ve got one tensor coming from the curvature and shiab operator, we have another tensor coming from the torsion and its augmentation.
[Eric checks his notes]
01:42:54
We’re doing okay.
Swervature and Swerve with Shiab Operators
01:43:06
Okay. We’re not doing physics yet. We’re just building tools. We’ve built ourselves a little bit of freedom, we have some reprieves, we’ve still got some very big debts to pay back for this magic beans trade. We’re in the wrong dimension. We don’t have good field content. We’re stuck on this one spinor. We’ve built ourselves some projection operators. We’ve picked up some symmetric, nonlinear \(\sigma\) field.
01:43:32
What can we write down in terms of equations of motion? Let’s start with Einstein’s concept. If we do shiab of the curvature tensor of a gauge potential, hit with an operator defined by the epsilon-sigma field, plus the star operator acting on the augmented torsion of the pair, this contains all of the information, when \(\pi\) is zero, in Einstein’s tensor.
$$ \bigcirc\kern-1.00em\circ\kern-0.62em·\text{}\kern0.3em_\varepsilon F_\pi +[\bigcirc\kern-1.00em\circ\kern-0.62em·\text{}\kern0.3em_\varepsilon T_{\varepsilon, \eta}, T_{\varepsilon, \pi}] + *T_{\varepsilon, \pi} = 0 $$
01:44:16
In other words, there is a spinorial analog of the Weyl curvature, a spinorial analog of the traceless Ricci curvature, and a spinorial analog of the scalar curvature. This operator should shear off the analog of the Weyl curvature just the way the Einstein’s projection shears off the Weyl curvature when you’re looking at the tangent bundle. And this term, which is now gauge invariant, may be considered as containing a piece that looks like \(\Lambda g_{\mu \nu}\), or a cosmological constant, and this piece here can be made to contain a piece that looks like Einstein’s tensor, and so this looks very much like the vacuum field equations. But we have to add in something else. I’ll be a little bit vague ’cause I’m still giving myself some freedom as we write this up.
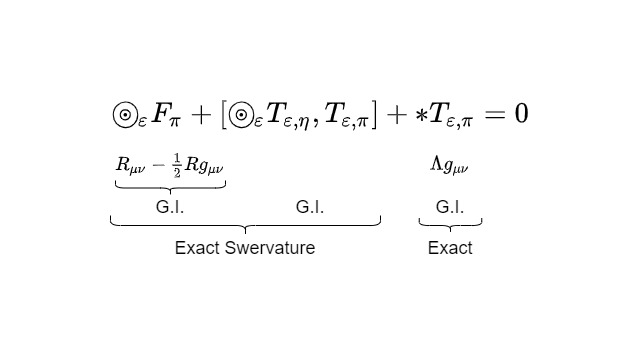
01:45:25
But we are going to define whatever tensor we need, for this term, for these terms here, this is gauge invariant, this is gauge invariant, and this is gauge invariant, with respect to the tilted gauge group. These two tensors together should be exact, and this tensor on its own should be exact.
01:45:53
We’re going to call the exact tensor the swervature. So the particular shiab operator we call the swerve, so that it’s swerve-curvature plus the adjustment needed for exactness, and another gauge invariant term which is not usually gauge invariant.
01:46:17
So that’s pretty cool. If that works, we’ve now taken the Einstein equation and we’ve put it not on the space of metrics, but we’ve put a generalization and an analog on the space of gauge potentials, much more amenable to quantization, with much more algebraic structure and symmetry in the form of the inhomogeneous gauge group and its homogeneous vector bundle, some of which may be supersymmetric.
Somatic Complex and Two More Operators
01:46:44
Now, the question is, we’ve integrated so tightly with the matter fields, we have to ask ourselves the question, “Can we see unification here?”
01:47:01
Let’s define matter content in the form of \(\Omega^0\) tensored in the spinors, which is a fancy way of saying spinors, together with a copy of the 1-forms tensored in the spinors. And let me come up with two other copies of the same data—so I’ll make \(\Omega^{d-1}\) just by duality, so imagine that there’s a Hodge star operator.
01:47:43
And, when I was a little kid, I had the Soma cube. I don’t know if you’ve ever played with one of these things, they’re fantastic. And I later found out that this guy who invented the Soma cube—which you had to put together as pieces—there was one piece that looked like this object. And he was like this amazing guy in the Resistance during World War II. So I would like to name this, the somatic complex after, I guess his name is Piet Hein. So this complex—I’m going to choose to start filling in some operators: the exterior derivative coupled to a connection, but in the case of spinors we’re going to put a slash through it. Let’s make this the identity.
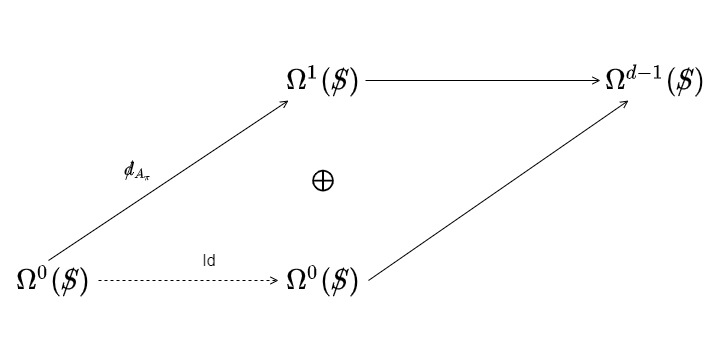
01:48:26
We’d now like to come up with a second operator here. And this second operator here should have the property that the complex should be exact and the obstruction to it being a true complex—to nilpotency—should be exactly the generalization of the Einstein equations, thus unifying the spinorial matter with the intrinsic replacement for the curvature equations.
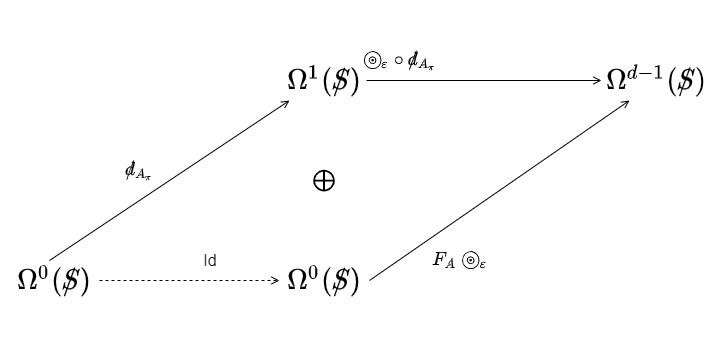
01:48:59
Well, we know that \(\unicode{x2215}\kern-0.5em \d_A\) composed with itself is going to be the curvature, and we know that we want that to be hit by a shiab operator. And if shiab is a derivation, you can start to see that that’s going to be curvature, so you want something like \(F_A\) followed by shiab over here to cancel. Then you think okay, how am I going to get at getting this augmented torsion? And, then you realize that the information in the inhomogeneous gauge group, you actually have information not for one connection, but for two connections.
01:49:44
So in one case, I can do plus star to pick up the \(A_{\pi}\). But I am also going to have a derivative operator if I just do a star operation, so I need another derivative operator to kill it off here. So I’m going to take minus the derivative with respect to the connection, which defines a connection 1-form as well as having the same derivative coming from the Levi-Civita connection on \(U\).
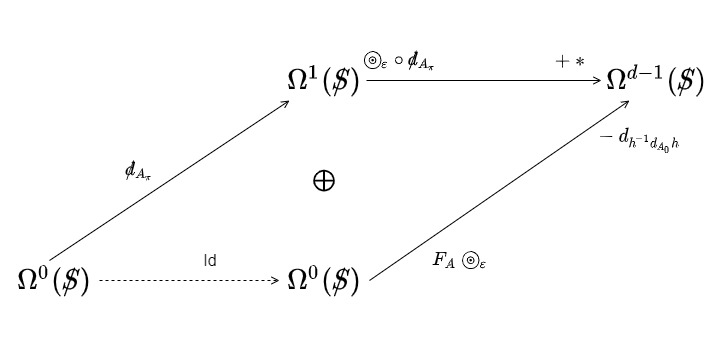
01:50:15
So in other words, I have two derivative operators here. I have two ad-value 1-forms. The difference between them has been to be a zeroth-order, and it’s going to be precisely the augmented torsion. And that’s the same game I’m going to repeat here.
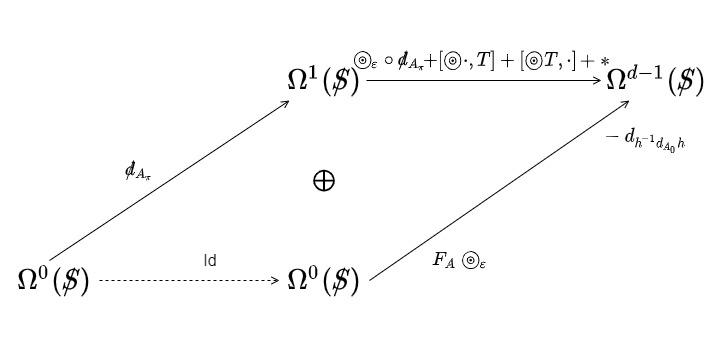
01:50:52
So I’m going to do the same thing here. I’m going to define a bunch of terms where, in the numerator, I’m going to pick up the \(\pi\) as well as the derivative, in the denominator, because I have no derivative here, I’m going to pick up this \(h^{-1} d_{A_0} h\).
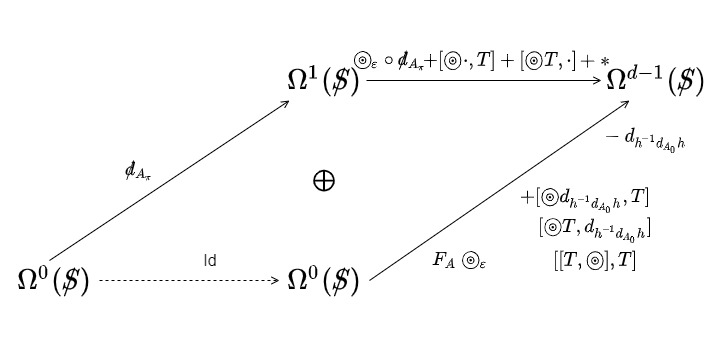
01:51:17
I’m going to do that again on the other side. There are going to be plus and minus signs, but it’s a magic bracket that knows whether or not it should be a plus sign or a minus sign and I apologize for that, but I’m not able to keep that straight. And then there’s going to be one extra term, where all these \(T\)s have the \(\varepsilon\) and \(\pi\)s.
01:51:50
Okay. So some crazy series of differential operators on the northern route… So if you take the high road or you take the low road, when you take the composition of the two, the differential operators fall out and you’re left with an obstruction term that looks like the Einstein field equation.
01:52:21
Well, that’s pretty good, if true. Can you go farther? Well, look at how close to this field content is to the picture from deformation theory that we learned about in low dimensions. The low-dimensional world works by saying that symmetries map to field content map to equations, usually in the curvature.
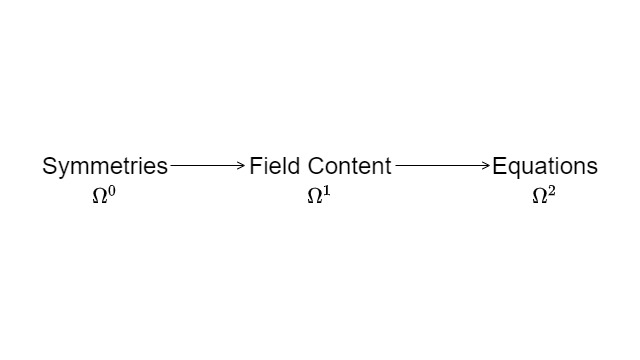
01:52:54
And when you linearize that, if you are in low enough dimension, you have \(\Omega^0\), \(\Omega^1\), sometimes \(\Omega^0\) again, and then something that comes from \(\Omega^2\), and if you can get that sequence to terminate by looking at something like a half-signature theorem or a bent back de Rham complex in the case of dimension three, you have an Atiyah-Singer theory. And remember we need some way to get out of infinite dimensional trouble, right? You have to have someone to call when things go wrong overseas and you have to be able to get your way home. And in some sense, we call on Atiyah and Singer and say we’re in some infinite dimensional space, can’t you cut out some finite dimensional problem that we can solve even though we start getting ourselves into serious trouble? And so we’re going to do the same thing down here. We’re going to have \(\Omega^0(ad)\), \(\Omega^1(ad)\), direct sum \(\Omega^0(ad)\), \(\Omega^{d−1}(ad)\), and it’s almost the same operators.
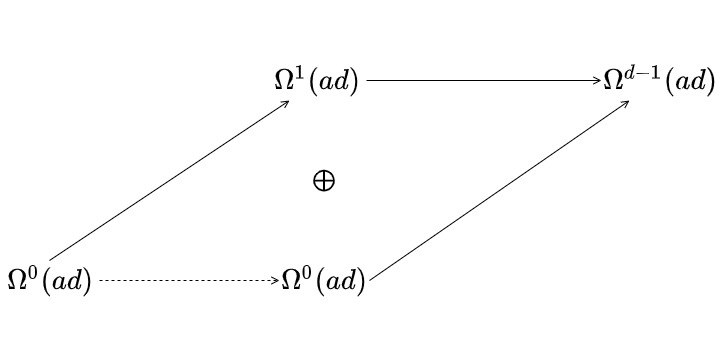
01:54:09
And this is now not just a great guess, it’s actually the information for the deformation theory of the linearized replacement of the Einstein field equations. So this is computing the Zariski tangent space just as if you were doing self-dual theory or Chern-Simons theory. You’ve got two somatic complexes, right? One of them is Bose, one of them is Fermi. The obstruction to both of them is a common generalization of the Einstein field equations. What’s more is if you start to think about this, this is some version of Hodge theory with funky operators. So you can ask yourself, “Well, what are the harmonic forms in a fractional spin context?”
01:55:03
Well, they’re different depending upon whether you take the degree-zero piece together with the degree-two piece, or you take the degree-one piece. Let’s just take the degree-one piece. You get some kind of equation—so, I’m going to decide that I have a \(\zeta\) field, which is an \(\Omega^1(\unicode{x2215}\kern-0.55em S)\), and a field \(\nu\), which always strikes me as a Yiddish field. \(\nu\) is \(\Omega^0(\unicode{x2215}\kern-0.55em S)\).
$$ \zeta \in \Omega^1(\unicode{x2215}\kern-0.55em S) $$
$$ \nu \in \Omega^0(\unicode{x2215}\kern-0.55em S) $$
01:55:47
What equation would they solve if we were doing Hodge theory relative to this complex? The equation would look something like this.
$$ *d_A^* \zeta = *\nu $$
01:56:10
There’d be one equation that was very simple, and then there’d be one equation that would be like really hard to guess.
$$ \bigcirc\kern-1.00em\circ\kern-0.62em·\text{}\kern0.3em_\varepsilon d_A \zeta + [\bigcirc\kern-1.00em\circ\kern-0.62em·\text{}\kern0.3em_\varepsilon\zeta, T] + [T, \bigcirc\kern-1.00em\circ\kern-0.62em·\text{}\kern0.3em_\varepsilon\zeta] + *\zeta = F_A \bigcirc\kern-1.00em\circ\kern-0.62em·\text{}\kern0.3em \nu + [[T, \nu], T] + [T, [T, \nu]] + [[T, \bigcirc\kern-1.00em\circ\kern-0.62em·\text{}\kern0.3em \nu], T] + *\nu $$
01:57:48
Now if you have something like that, that would be a hell of a Dirac equation. Right? You’ve got differential operators over here. You’ve got differential operators—I guess I didn’t write them in—but you would have two differential operators over here, and you’d have this differential operator coming from this Maurer-Cartan form. So I apologize, I’m being a little loose here, but the idea is you have two of these terms are zeroth-order, three of these terms would be first-order, and on this side (the left side), one term would be first-order.
01:58:27
And that’s not there, that was a mistake. Oh no, sorry. That was a mistake, calling it a mistake. These are two separate equations, right? So you have two separate fields, \(\nu\) and \(\zeta\), and you have a coupled set of differential equations that are playing the role of the Dirac theory, coming from the Hodge theory of a complex, whose obstruction to being [a] cohomology theory would be the replacement to the Einstein field equations, which would be rendered gauge invariant on a group relative to a tilted subgroup.
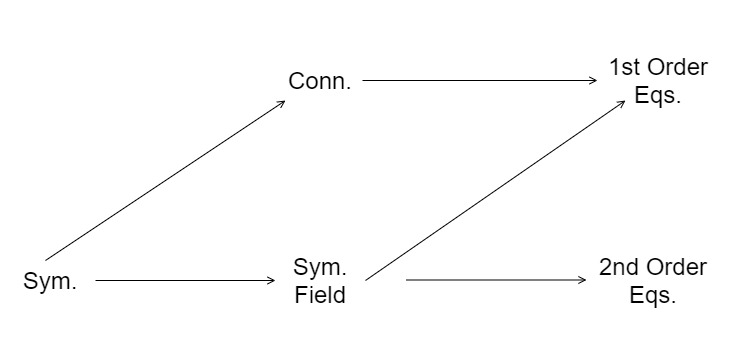
01:59:12
So now we’ve dealt with two of the three sectors. Is there any generalization of the Yang-Mills equation? Well, if we were to take the Einstein field equation generalization and take the norm square of it—oh, there’s some point I should make here, just one second. I’ve been treating this as if everything is first-order, but what really happens here is that you’ve got symmetries. You’ve got symmetric field content, you’ve got ordinary connections, and we’re neglecting to draw the fact that there have to be equations here too. These equations are first-order. So why do we get to call this a first-order theory if there are equations here which are of second-order? Well, it’s not a pure first-order theory, but when I say a first-order theory in this context, what I really mean is that the second-order equations are completely redundant on the first-order equations by virtue of the symmetry principle. That is, any solution of the first-order equation should automatically imply a solution of the second-order equations. So from that perspective, I can pretend that this isn’t here because it is sufficient to solve the first-order equations.
02:00:49
So I can now look—let’s call that entire replacement, which we previously called \(\alpha\), I’m going to set \(\alpha\) equal to \(\Upsilon\), because I’ve actually been using \(\Upsilon\), the portion of it that is just the first-order equations, and take the norm squared of that, that gives me a new Lagrangian. And if I solve that new Lagrangian, it leads to equations of motion that look like exactly what we said before.
$$ \alpha = \Upsilon $$
$$ ||\Upsilon||^2 \rightarrow \delta^\omega(\mathscr{D}_2^\omega \circ \mathscr{D}_1^\omega) $$
02:01:28
And it ends up defining an operator that looks something like this, \(d_A^∗\) the adjoint of the shiab operator.
$$ *(d_A^* \bigcirc\kern-1.00em\circ\kern-0.62em·\text{}\kern0.3em^* + * + …)(\bigcirc\kern-1.00em\circ\kern-0.62em·\text{}\kern0.3em_\varepsilon F_{A_\pi} + …) $$
02:02:01
So in other words, this piece gives you some portion that looks like, right, from the swervature tensor there’s going to be some component that’s playing the role of Einstein’s field equations directly, and the Ricci tensor, but generalized. And then you’re going to have some differential operator here, so that the replacement for the Yang-Mills term, instead of \(d^∗_A F_A\), you’ve got these two shiab and an adjoint shiab together in the center, generalizing the Yang-Mills theory. Then you say well, how come we don’t just see the Yang-Mills theory? Why don’t we see general relativity as well? But in the full expansion there’s also a term that’s zeroth-order that’s effectively acting like the identity which hits this as well. So you have one piece that looks like the Yang-Mills theory, and in these second-order equations you also have a piece that looks like the Einstein theory. And this is in the vacuum equations. So then the question is how do you see the Dirac theory coming out of this?
02:03:07
And so what we’re just trying to put together now before we come out with the manuscript for this is, putting these two elliptic complexes together, the Dirac terms go between the two complexes, right? So the idea is that the stress-energy tensor should be the up-and-back term and the Dirac equations should come out of the term that goes up-and-over versus the term that goes over-and-up, and you need some cancellations to make sure that everything is of zeroth-order, properly invariant, etc. And that’s taking a little time because frankly, I’m not good at keeping track of indices, minus signs, left-right—it’s a learning-disabled nightmare.
Matter in Unified Field Content
02:03:53
So, we’ve got one more unit to go. I mean, there’s a fifth unit that has to do with mathematical applications, but this is sort of a physics talk for today. Is there any question before we go into the last unit and then really handle questions for real? All right, let me show you the next little bit.
02:04:18
We’ve got problems. We’re not in four dimensions, we’re in 14. We don’t have great field content because we’ve just got these unadorned spinors, and we’re doing gauge transformations effectively on the intrinsic geometric quantities, not on some safe auxiliary data that’s tensor producted with what our spinors are. How is it that we’re going to find anything realistic? And then we have to remember everything we’ve been doing recently has been done on \(U\). We’ve forgotten about \(X\). How does all of this look to \(X\)?
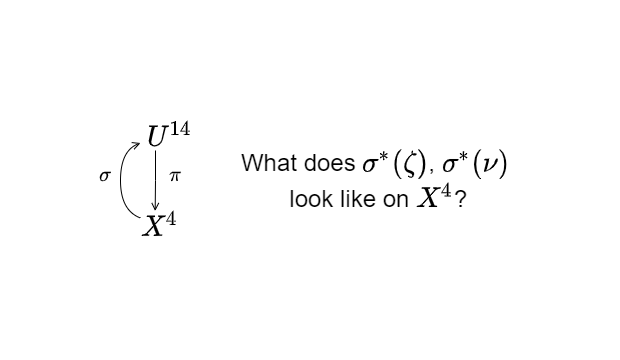
02:05:04
So \(X\) is sitting down here, and all the action is happening up here on \(U^{14}\). There’s a projection operator—I’ve used \(\pi\) twice, it’s not, here, the field content, it’s just projection. And I’ve got a \(\sigma\), which is a section. What does \(\zeta\) pulled back or \(\nu\) pulled back look like on \(X^4\)?
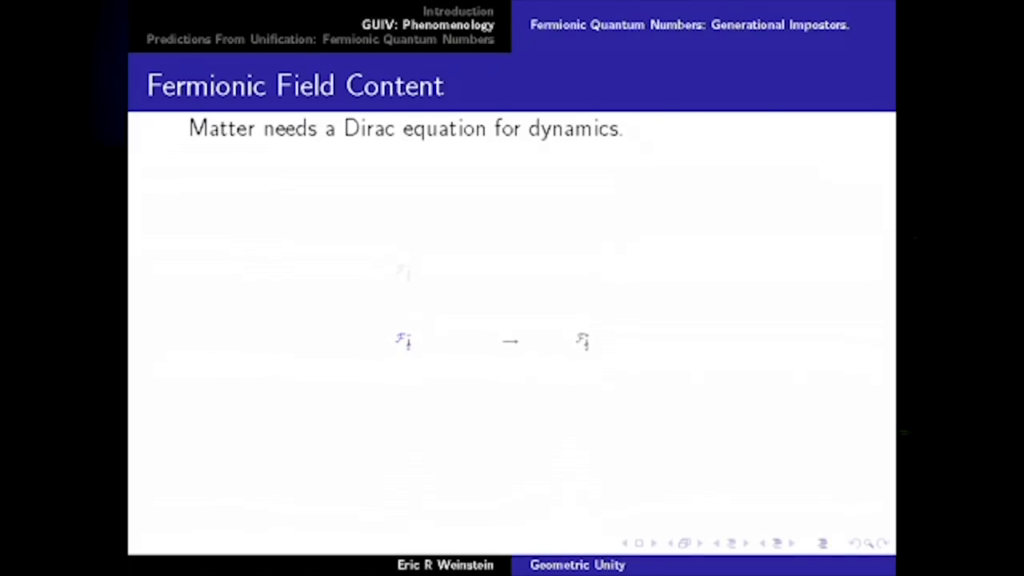
02:06:05
Okay. Let’s try to think about how we would come up with this field content starting from first principles. Let’s imagine that there’s nothing to begin with. Then you have one copy of matter: whatever it is that we see in our world, the first generation. In order for that to become interesting, it has to have an equation, so it has to get mapped somewhere.
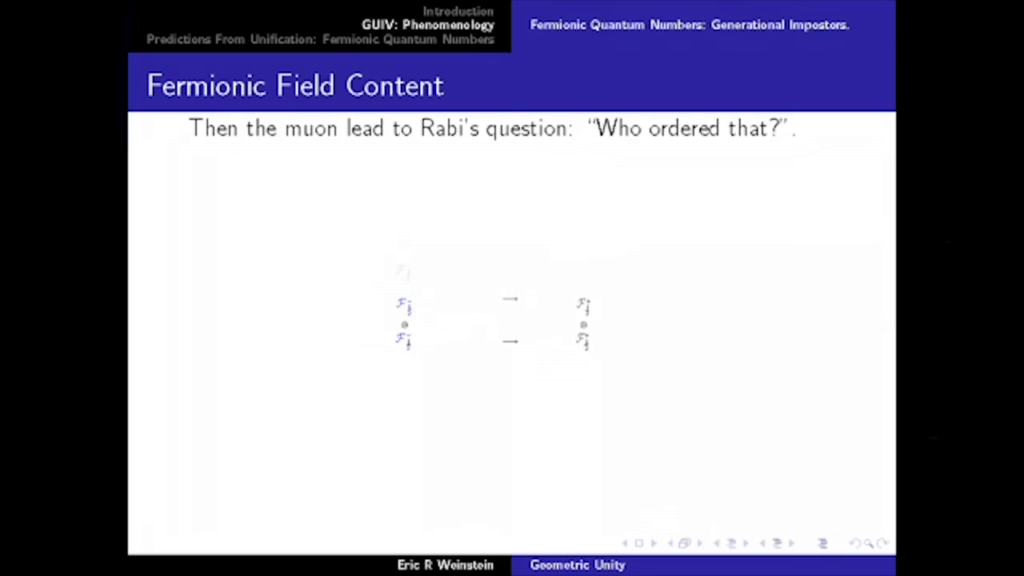
02:06:37
Then we see the muon and all the rest of the matter that comes with it, and we have a second generation.

02:06:44
Then in the mid-1970s, [Martin Lewis] Perl finds the tau particle, and we start to get panicked that we don’t understand what’s going on.
Third Generation is an Imposter
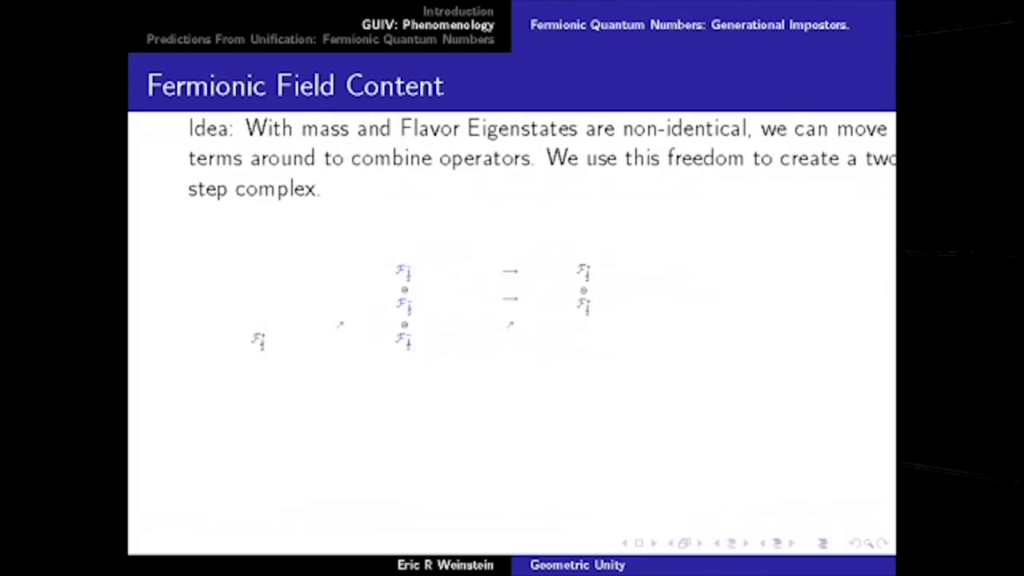
02:06:54
One thing we could do is we could move these equations around a little bit and move the equation for the first generation back, and then we can start adding particles. Let’s imagine that we could guess what particles we’d add.


02:07:10
We’d add a pseudo-generation of 16 particles, spin-3/2, never before seen. Not necessarily superpartners, but Rarita-Schwinger matter with familiar internal quantum numbers, but potentially, so that they’re flipped, so that matter looks like anti-matter to this generation. Then we add, just for the heck of it, 144 spin-1/2 fermions, which contain a bunch of particles with familiar quantum numbers, but also some very exotic looking particles that nobody’s ever seen before.



02:07:46
Now we start doing something different. We make an accusation. One of our generations isn’t a regular generation: it’s an impostor. At low energy, in a cooled state, potentially, it looks just the same as these other generations, but were we somehow able to turn up the energy, imagine that it would unify differently with this new matter that we’ve posited rather than simply unifying onto itself. So two of the generations would unify onto themselves, but this third generation would fuse with the new particles that we’ve already added. We consolidate geometrically. We can add some zeroth-order terms, and we imagine that there is an elliptic complex that would govern the state of affairs.
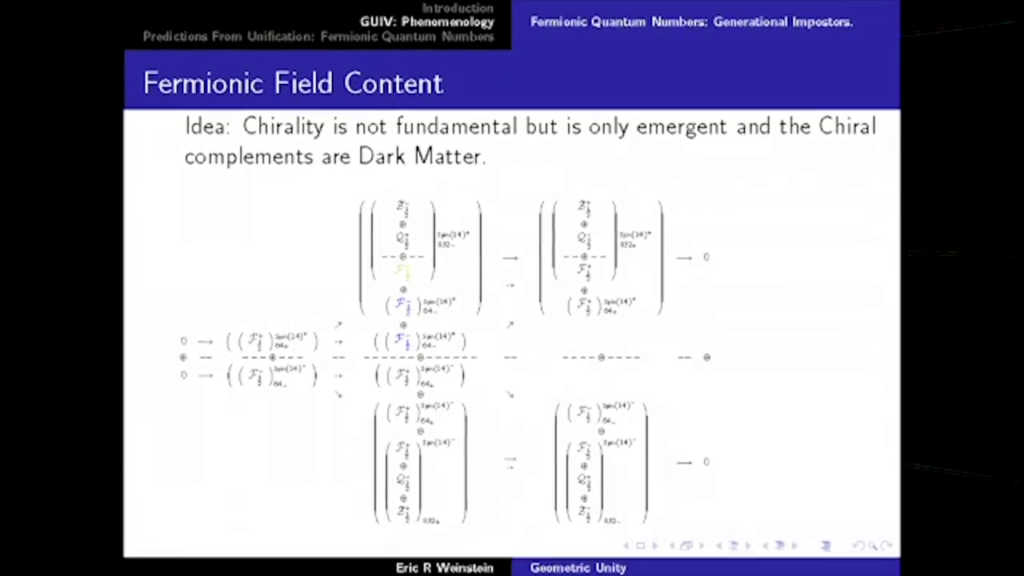
02:08:36
We then choose to add some stuff that we can’t see at all, that’s dark. And this matter would be governed by forces that were dark too. There might be dark electromagnetism, and dark strong, and dark weak. It might be that things break in that sector completely differently, and it doesn’t break down to an \(\text{SU}(3) \times \text{SU}(2) \times \text{U}(1)\) because these are different \(\text{SU}(3)\)s, \(\text{SU}(2)\)s, and \(\text{U}(1)\)s, and it may be that there would be like a high energy \(\text{SU}(5)\), or some Pati-Salam model. Imagine then that chirality was not fundamental, but it was emergent—that you had some complex, and as long as there were cross terms these two halves would talk to each other. But if the cross terms went away, the two terms would become decoupled.
02:09:22
And just the way we have a left hand and we have a right hand, and you ask me, right, imagine you have a neurological condition in an Oliver Sacks sort of an idiom, if somebody is only aware of one side of their body and they say, “Oh my God, I’m deformed, I’m asymmetric!” But we actually have a symmetry between the two things that can’t see each other. Then we would still have a chiral world, but the chirality wouldn’t be fundamental. There’d be something else keeping the fermions light, and that would be the absence of the cross terms. Now if you look at what happens in our replacement for the Einstein field equations, the term that would counterbalance the scalar curvature, if you put these equations on a sphere, they wouldn’t be satisfied if the \(T\) term had a zero expectation value: because there would be non-trivial scalar curvature in the swervature terms, but there’d be nothing to counterbalance it. So it’s fundamentally the scalar curvature that would coax the VEV (vacuum expectation value) on the augmented torsion out of the vacuum to have a non-zero level. And if you pumped up that sphere and it smeared out the curvature, which you can’t get rid of because of topological considerations—let’s say from Chern-Weil theory—you would have a very diffuse, very small term. And that term would be the term that was playing the role of the cosmological constant.
02:10:44
So in a large universe, you’d have a curvature that was spread out, and things would be very light, and things would get very dark due to the absence of curvature linking the sectors. And that turns out to be exactly our complex.
Lecture Conclusion
02:11:07
So in other words, just to recap, starting with nothing other than a four-manifold, we built a bundle \(U\). The bundle \(U\) had no metric, but it almost had a metric. It had a metric up to a connection. There was another bundle on top of that bundle called the chimeric bundle. The chimeric bundle had an intrinsic metric. We built our spinors on that. We restricted ourselves to those spinors. We moved most of our attention to the emergent metric on \(U^{14}\), which gave us a map between the chimeric bundle and the tangent bundle of \(U^{14}\). We built a toolkit, allowing us to choose symmetric field content, to define equations of motion on the cotangent space of that field content, to form a homogeneous vector bundle with the fermions, to come up with unifications of the Einstein field equations, Yang-Mills equations, and Dirac equations. We then broke those things apart under decomposition, pulling things back from \(U^{14}\), and we found a three-generation model where nothing has been put in by hand, and we have a 10-dimensional normal component, which looks like the \(\text{Spin}(10)\) theory.
02:12:34
I can tell you where there are problems in this story. I can tell you that when we moved from Euclidean metric to Minkowski metric, we seem to be off by a sign somewhere, or I could be mistaken. I could tell you that the propagation in 14 dimensions has to be worked out so that we would be fooled into thinking we were on a four-dimensional world. There are lots of things to ask about this theory. But I find it remarkable that, tying our hands, we find ourselves with new equations, unifications, and three generations in a way that seems surprisingly rich, certainly unexpected… And I think I’ll stop there. Thank you very much for your time.
PowerPoint

02:13:24
So, thanks for watching that video. What I thought I would do, since that was the first time I’d really presented the theory at all in public, and I had gotten somewhat turned around on my trip to England and trying, probably stupidly, to do last-minute corrections got me a bit confused in a few places, and I wrote some things on the board I probably shouldn’t have, I thought I would try a partial explainer for technically-oriented people so that they’re not mystified by the video. And any errors here are my own, I’m known to make many. So, hopefully they won’t be too serious, but we’ll find out. So this is a supplementary explainer for the Geometric Unity talk at Oxford that you just saw.
Preliminary

02:14:15
First of all, I think the most important thing to begin with is to ask what new hard problems arise when you’re trying to think about a fundamental theory that aren’t found in any earlier theory. Now, every time you have an effective theory, which is a partial theory, there is always the idea that you can have recourse to a lower-level strata. So you don’t have to explain, in some sense, everything coming from very little, or nothing. I think that the really difficult issue that people don’t talk enough about is the problem of the fire that lights itself. And I think this was beautifully demonstrated by M.C. Escher in his famous lithograph Drawing Hands, where he takes the idea of the canvas, or the paper, as a given, but somehow he imagines that the canvas could will into existence the ink needed to draw the hands that move the pen that draw the hands. That concept is actually the super tricky part, in my opinion, about going from effective theories to any attempt at a fundamental theory. So, with that said, what I want to think about is what antecedents does this concept have in physics? And I find that there really aren’t any candidate theories of everything, or unified field theories, that I can find that plausibly give us an idea of how a canvas would will an entire universe into being. And so, that really, to me, is the conceptual problem that I think bedevils this, and makes the step quite a bit more difficult than some of the previous technical steps.
02:15:59
If you ask for antecedents, however, there is one that, at least within physics, is relatively famous, and that is by John Archibald Wheeler. And it is a picture, in some sense, of the universe contemplating itself. And so this idea that somehow the universe would contemplate itself into existence, maybe the letter U is in some sense analogous to the paper, and somehow the eye, rather than the hand, is drawn across to look at a different part of the U. And, whether or not that has meaning is intrinsically always a question. People are animated by it, but I don’t know that people have actually worked on it. The quote of Einstein’s I think that really speaks to me often the most, and maybe even was my thesis problem, was he asked whether the creator had any choice in how the universe was constructed. And so I think if you believe that the canvas is itself that which generates all of the content and all of the action, you’re left with a puzzle as to how would you move forward from this? It might be easier, in a mathematical sense, to temporarily put the U on its back to put it more in line with a standard picture that many mathematicians and physicists will be familiar with.
Sector I: The Observerse

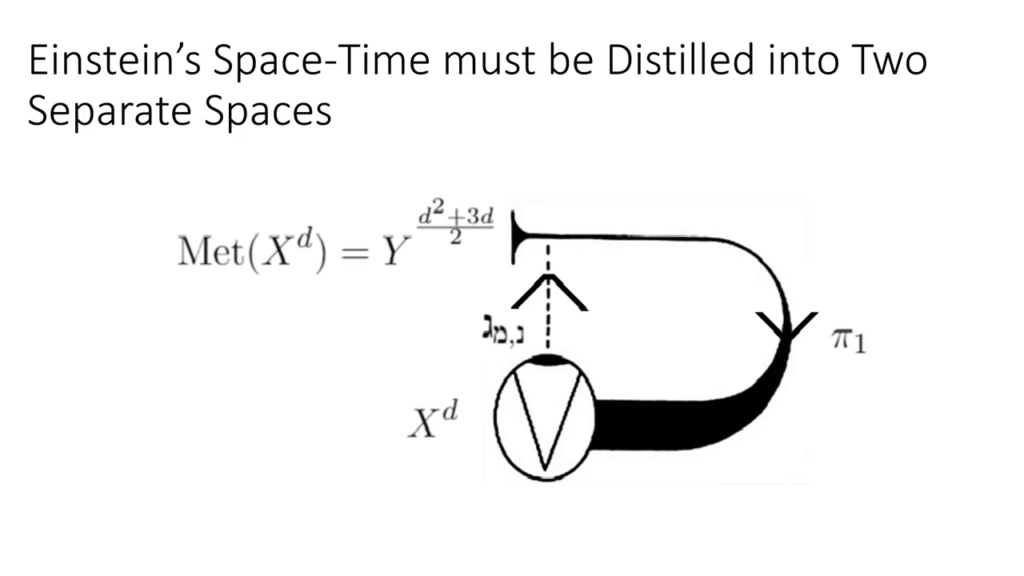
02:17:28
In sector I of the Geometric Unity theory, spacetime is replaced and recovered by the observerse contemplating itself. And so, there are several sectors of GU, and I wanted to go through at least four of them. In Einstein’s spacetime, we have not only four degrees of freedom, but also a spacetime metric representing rulers and protractors. If we’re going to replace that, it’s very tricky, because it’s almost impossible to think about what would be underneath Einstein’s theory.
02:18:03
Now there’s a huge problem in the spinorial sector, which I don’t know why more people don’t worry about, which is that spinors aren’t defined for representations of the double cover of \(\text{GL}(4, \mathbb{R})\), the general linear group’s effective spin analog. And as such, if we imagine that we will one day quantize gravity, we will lose our definition, not of the electrons but, let’s say, of the medium in which the electrons operate. That is, there will be no spinorial bundle until we have an observation of a metric. So, one thing we can do is to take a manifold \(X^d\) as the starting point and see if we can create an entire universe from no other data—not even with a metric. So, since we don’t choose a metric, what we instead do is to work over the space of all possible point-wise metrics. So not quite in the Feynman sense, but in the sense that we will work over a bundle that is of a quite larger, quite a bit larger dimension.
02:19:09
So for example, if \(X\) was four-dimensional, therefore \(d = 4\), then \(Y\) in this case would be \(d^2\), which would be \(16 + 3d\), which would be 12, making 28, divided by 2, which would be 14. So in other words, a four-dimensional proto-spacetime—not a spacetime, but a proto-spacetime with no metric—would give rise to a 14-dimensional observerse portion called \(Y\). Now I believe that in the lecture in Oxford I called that \(U\), so I’m sorry for the confusion, but of course, this shifts around every time I take it out of the garage, and that’s one of the problems with working on a theory in solitude for many years.
02:19:57
So we have two separate spaces, and we have fields on the two spaces. Now what I’m going to do is I’m going to refer to fields on the \(X^d\) space by Hebrew letters. So instead of \(g_{\mu \nu}\) for a metric, I just wrote \(ℷ_{נ,מ}\) (gimel mem nun). And the idea being that I want to separate Latin and Greek fields on the \(Y\) space from the rather rarer fields that actually live directly on \(X\).
02:20:26
So, this is a little bit confusing. One way of thinking about it is to think of the observerse as the stands plus the pitch in a stadium. I think I may have said that in the lecture, but this is what replaces the questions of “Where” and “When” in the newspaper story that is a fundamental theory. “Where” and “When” correspond to space and time, “Who” and “What” correspond to bosons and fermions, and “How” and “Why” correspond to equations and the Lagrangian that generates them. So, if you think about those six quantities, you’ll realize that that’s really what the content of a fundamental theory is, assuming that it can be quantized properly.
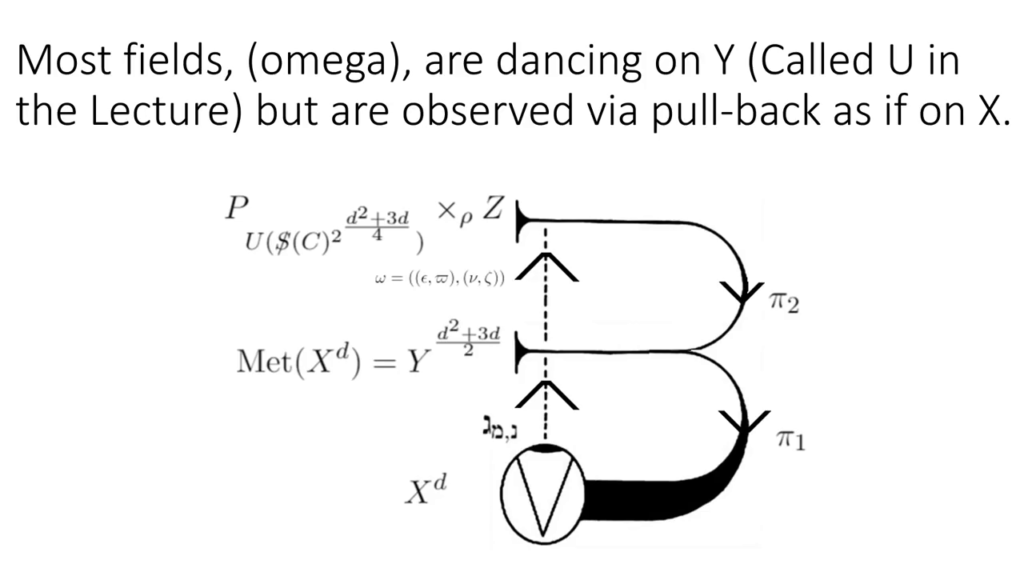
02:21:07
Most fields—and in this case we’re going to call the collection of 2-tuples \(\omega\), so inside of \(\omega\) that will be, in the first tuple we’ll have \(ϵ\) and \(ϖ\), written in sort of a nontraditional variation of how we write this symbol for \(\pi\); in the second tuple, we’ll have the letters, \(\nu\) and \(\zeta\), and I would like them not to move because they honor particular people who are important. So most fields, in this case \(\omega\), are dancing on \(Y\), which was called \(U\) in the lecture, unfortunately. But, they are observed via pullback as if they lived on \(X\). In other words, if you’re sitting in the stands, you might feel that you’re actually literally on the pitch, even though that’s not true. So what we’ve done is we’ve taken the U of Wheeler, we’ve put it on its back, and created a double-U structure.
02:21:59
And the double-U structure is meant to say that there’s a bundle on top of a bundle. Again, Geometric Unity is more flexible than this, but I wanted to make the most concrete approach to this possible for at least this introduction. Sometimes, we don’t need to state that \(Y\) would, in fact, be a bundle. It could be an immersion of \(X\) into any old manifold, but I’d like to go with the most ambitious version of GU first.
02:22:27
So, the two projection maps are \(\pi_2\) and \(\pi_1\), and what we’re going to say up top is that we’re going to have a symbol \(Z\) and an action of a group \(\rho\) on \(Z\), standing in for any bundle associated to the principal bundle, which is generated as the unitary bundle of the spinors on the chimeric tangent bundle to \(Y\). It’s a bit of a mouthful, but the key issue was that on the manifold \(Y\), there happens to be a bundle which is isomorphic, non-canonically, to the tangent bundle of \(Y\), which has a definite and canonical metric. And in fact, that carries the spinors. So this is the way in which we get spinors without ever having to choose a metric, but we pick up some technical debt, to use the computer science concept, by actually having to now work on two different spaces, \(X\) and \(Y\), and we’re not merely working on \(X\) anymore.
Sector II: Unified Field Content

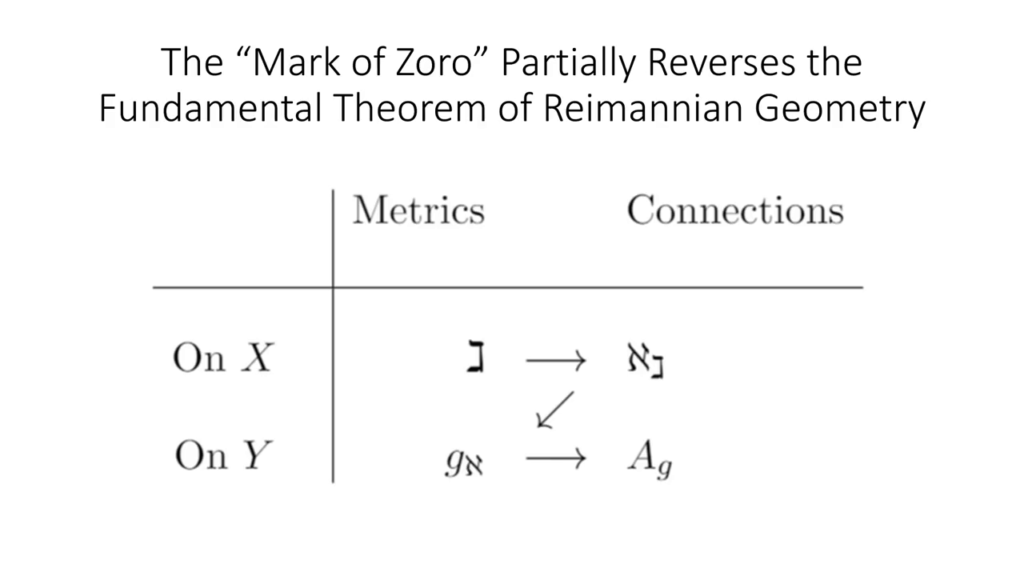
02:23:30
This leads to the Mark of Zorro. That is, we know that whenever we have a metric, by the fundamental theorem of Riemannian geometry we always get a connection. It happens, however, that what is missing to turn the canonical chimeric bundle on \(Y\) into the tangent bundle of \(Y\) is, in fact, a connection on the space \(X\).
02:23:52
So, there is one way in which we’ve reversed the fundamental theorem of Riemannian geometry, where a connection on \(X\) leads to a metric on \(Y\). So if we do the full transmission mechanism out, \(ℷ\) on \(X\) leads to \(\aleph_ℷ\) for the Levi-Civita connection on \(X\). \(\aleph_{ℷ}\) leads to \(g_{\aleph}\), which is—sorry, \(g_\aleph\). I’m not used to using Hebrew in math.* So \(g_{\aleph}\), then, is a metric on \(Y\), and that creates a Levi-Civita connection of the metric on the space \(Y\) as well, which then induces one on the spinorial bundles. In sector II, the inhomogeneous gauge group on \(Y\) replaces the Poincaré group and the internal symmetries that are found on \(X\). And in fact, you use a fermionic extension of the inhomogeneous gauge group to replace the supersymmetric Poincaré group, and that would be with the field content 0-forms tensored with spinors direct sum 1-forms tensored with spinors all up on \(Y\) as the fermionic field content.
* Note: Where Eric mistakes \(\alpha\) for \(\aleph\) it is written correctly in the transcript for the sake of clarity and parity with the diagram.
02:25:09
So that gets rid of the biggest problem, because the internal symmetry group is what causes the failure, I think, of supersymmetric particles to be seen in nature, which is we have two different origin stories, which is a little bit like Lilith and Genesis. We can’t easily say we have a unified theory if spacetime and the \(\text{SU}(3) \times \text{SU}(2) \times \text{U}(1)\) group that lives on spacetime have different origins and cannot be related. In this situation, we tie our hands and we have no choice over the group content.

02:25:46
So just to fix bundle notation, we let \(H\) be the structure group of a bundle \(P_H\) over a base space \(B\). We use \(\pi\) for the projection map. We’ve reserved the variation in the \(\pi\) orthography for the field content, and we try to use right principal actions. I’m terrible with left and right, but we do our best. We use \(H\) here, not \(G\), because we want to reserve \(G\) for the inhomogeneous extension of \(H\) once we move to function spaces.

02:26:23
So with function spaces, we can take the bundle of groups using the adjoint action of \(H\) on itself and form the associated bundle, and then move to \(C^\infty\) sections to get the so-called gauge group of automorphisms. We have a space of connections, typically denoted by \(\mathcal{A}\), and we’re going to promote \(\Omega^1(B,\text{ ad}(P_H))\) to a notation of script \(\mathcal{N}\) as the affine group, which acts directly on the space of connections.

02:27:07
Now, the inhomogeneous gauge group is formed as the semi-direct product of the gauge group of automorphisms together with the affine group of translations of the space of connections. And you can see here is a version of an explicit group multiplication rule, I hope I got that one right.

02:27:27
And then we have an action of \(\mathcal{G}\), that is the inhomogeneous gauge group, on the space of connections, because we have two different ways to act on connections. We can either act by gauge transformations or we can act by affine translations. So putting them together gives us something for the inhomogeneous gauge group to do.


02:27:46
We then get a bi-connection. In other words, because we have two different ways of pushing a connection around, if we have a choice of a base connection, we can push the base connection around in two different ways according to the portion of it that is coming from the gauge transformations of curly \(\mathcal{H}\) or the affine translations coming from curly \(\mathcal{N}\). We can call this map the bi-connection, which gives us two separate connections for any point in the inhomogeneous gauge group. And we can notice that it can be viewed as a section of a bundle over the base space to come when we find an interesting embedding of the gauge group that is not the standard one in the inhomogeneous gauge group.

02:28:42
So our summary diagram looks something like this. Take a look at the \(\tau_{A_0}\). We will find a homomorphism of the gauge group into its inhomogeneous extension that isn’t simply inclusion under the first factor. We—and I’m realizing that I have the wrong pi projection, that should just be a simple \(\pi\) projecting down. We have a map from the inhomogeneous gauge group via the bi-connection to \(\mathcal{A} \times \mathcal{A}\), connections cross connections, and that behaves well according to the difference operator \(\delta\) that takes the difference of two connections and gives an honest ad-valued 1-form.

02:29:23
The infinitesimal action of a gauge transformation, or at least an infinitesimal one, on a point inside of the group is given by a somewhat, almost familiar expression, which should remind us of how the first term in the gauge deformation complex for self-dual Yang-Mills actually gets started. And so, by acting via this interesting embedding of the gauge group inside its inhomogeneous extension, but the non-trivial one, we get something very close to the original first step of the two-step deformation complex.
Sector III: Toolkit for the Unified Field Content

02:30:09
Now, in sector III, there are payoffs to the magic beans trade. The big issue here is that we’ve forgone the privilege of being able to choose and dial in our own field content, and we’ve decided to remain restricted to anything we can generate only from \(X^d\), in this case \(X^4\). So we generated \(Y^{14}\) from \(X^4\), and then we generated chimeric tangent bundles on top of that. We built spinors off of the chimeric tangent bundle, and we have not made any other choices. So we’re dealing with, I think it’s \(U^{128}\), \(U^{2^7}\). That is our structure group, and it’s fixed by the choice of \(X^4\), not anything else.

02:30:58
So, what do we get? Well as promised, there is a tilted homomorphism, which takes the gauge group into its inhomogeneous extension. It acts as inclusion on the first factor, but it uses the Levi-Civita connection to create a second sort of Maurer-Cartan form. I hope I remember the terminology right. It’s been a long time. The map is injective because it’s injective under the first factor, but it actually gives us a nontrivial embedding of the gauge group in its inhomogeneous extension, which makes the whole theory work.
Shiab Operators

02:31:34
We then get to shiab operators. Now, a shiab operator is a map from the group crossed the ad-valued \(i\)-forms. In this case, the particular shiab operator we’re interested in is mapping \(i\)-forms to \((d – 3 + i)\)-forms. So for example, you would map a 2-form to \(d – 3 + i\). So if \(d\), for example, were 14, and \(i\) were equal to 2, then 14 minus 3 is equal to 11 plus 2 is equal to 13. So that would be an ad-valued \((14 – 1)\)-form, which is exactly the right place for something to form a current, that is, the differential of a Lagrangian on the space.


02:32:38
Now the augmented torsion, the torsion is a very strange object. It’s introduced sort of right at the beginning of learning differential geometry, but it really doesn’t get used very much. One of the reasons it doesn’t get used in gauge theory is that it’s not gauge invariant. It has a gauge invariant piece to it, but then a piece that spoils the gauge invariance. But because we have two connections, one of the ideas was to introduce two diseases and then to take a difference, and as long as the disease is the same in both, the difference will not have the disease because both diseases are included but with a minus sign between them.
02:33:13
So the augmented torsion is relatively well behaved, relative to this particular slanted, or tilted, embedding of the gauge group in its inhomogeneous extension. This is very nice, because now we actually have a use for the torsion. We have an understanding of why it may never have figured, particularly into geometry, is that you need two connections rather than one to see the advantages of torsion at all.

02:33:43
So here’s an example of one ship in a bottle (shiab) operator. I think this would be sort of analogous, if I’m not mistaken, to trying to take the Ricci curvature from the entire Riemann curvature. But if you think about what Einstein did, Einstein had to go further and reduce the Ricci curvature to the scalar curvature, and then sort of dial the components of the traceless Ricci and the scalar curvature to get the right proportions. So, there are many shiab operators, and you have to be very careful about which one you want. And once you know exactly what it is you’re trying to hit, you can choose the shiab operator to be bespoke and get the contractions that you need.
02:34:29
Now, I’ve made you guys sit through a lot, so I wanted to give you, sort of humorously, a feeling of positivity for the exhaustion:
02:34:42
“The years of anxious searching in the dark, with their intense longing, their intense alternations of confidence and exhaustion and the final emergence into the light—only those who have experienced it can understand it.” -Albert Einstein
02:34:41
I’ve just always thought this was, like, the most sensitive and beautiful quote, and I wish it were one of his better known quotes, but I think it’s so singular that it’s hard to, it’s hard to feel what it was that he was talking about because, in fact, he sort of explains this in the last line.
GU Equations: Swervature and Displasion

02:35:10
So, given that you’ve been on a long journey, here is something of what Geometric Unity equations might look like. So in the first place, you have the swerved curvature, the shiab applied to the curvature tensor. That, in general, does not work out to be exact, so you can’t have it as the differential of a Lagrangian. And in fact, you know, we talked about swirls, swerves, twirls, eddies—there has to be a quadratic eddy tensor, that I occasionally forget when I pull this thing out of mothballs, and the two of those together make up what I call the total swervature. And, on the other side of that equation, you have the displaced torsion, which I’ve called the displasion. And to get rid of the pesky, sort of, minus sign and Hodge star operator… This would be the replacement for the Einstein equation, not on \(X\) where we would perceive it, but on \(Y\) before being pulled back onto the manifold \(X\).

02:36:12
So, a condensation of that would be very simple. In simplest terms, we would be saying that the swervature is equal to the displasion, and at least in this sector of the four main equations of theoretical physics, this would be the replacement for the Einstein equations, again on \(Y\) before being pulled back to \(X\).
Sector IV: Fermionic Field Content

02:36:33
Next is the sketch of the fermionic field content. I’m not sure whether that should have been sector IV or sector III, but it’s going to be very brief. I showed some pictures during the lecture, and I’m not going to go back through them, but I wanted to just give you an idea of where this mysterious third generation I think comes from.

02:36:55
So, if we review the three identities here, we see that if we have a space \(V\), thought of like as a tangent bundle, and then you have spinors built on the tangent bundle, when you tensor product the tangent bundle with its own spinors, it breaks up into two pieces. One piece is the so-called Cartan product, which is sort of the sum of the highest weights, and the other is a second copy of the spinors gotten through the Clifford contraction. So, that’s well known, but now what I think fewer people know—many people know that the spinors have a sort of an exponential property. That is, the spinors of a direct sum are the tensor product of the spinors of the two summands of the direct sum. So that’s a very nice sort of version of an exponential—an exponential would take a sum and turn it into a product.
02:37:52
What happens when you’re trying to think about a tangent space in \(Y\) as being broken up into a tangent space along an immersed \(X\), together with its normal bundle? So imagine that \(X\) and \(Y\) are the tangent space to \(X\) and a normal bundle. So the Rarita-Schwinger piece—that is, the spin-3/2 piece—has a funny kind of an almost exponential property. That is, the Rarita-Schwinger content of a direct sum of vector spaces is equal to the Rarita-Schwinger of the first, tensor producted with the ordinary spinors in the second, direct sum with the ordinary spinors in the first, tensor producted with the Rarita Schwinger content of the second summand. But then there’s this extra interesting term, which is the spinors on the first summand tensor producted with the spinors on the second summand.
02:38:53
Now recalling that, when I started my career, we did not know that neutrinos were massive. And I figured that they probably had to be massive because I desperately wanted a 16-dimensional space of internal quantum numbers, not 15, because my ideas only work if the space of internal quantum numbers is of dimension \(2^n\). And, one of my favorite equations at the time was \(15 = 2^4\). Not literally true, but almost true. And thankfully in the late 1990s, the case for 16 particles in a generation was strengthened when neutrinos were found to have mass. But that remaining term in the southeast corner, the spinors on \(X\) tensor spinors on \(Y\) looks like the term above it in line 2.15. And that, in fact, is the third generation of matter, in my opinion. That is, it is not a true generation. It is broken off, and would unify very differently if we were able to heat the universe to the proper temperature.

02:40:04
So, starting to sum up, this is not the full theory. I’m just presenting this in part to dip my toe back into the water. It’s a daunting task to try to address people about something you’ve been thinking about for a long time and have no idea whether it’s even remotely correct.
02:40:19
This is the Einsteinian replacement, and it must be pulled back to \(X\). That’s the first thing.
02:40:24
The Yang-Mills/Maxwell piece comes from a “Dirac square” of the Einstein replacement. That is, I don’t believe that we’re really looking for a unifying equation. I think we’re looking for a unifying Dirac square. Dirac famously took the square root of the Klein-Gordon equation, and he gave us the Dirac equation. And in fact, I believe that the Dirac equation and the Einstein equation are to be augmented and fit into the square root part of a Dirac square. And I believe that the Yang-Mills content and Higgs version of the Klein-Gordon equation would go in the square part of the Dirac square. So, two of these equations unify differently than two others, and the two pairs are unified in the content of a Dirac square.
02:41:16
The Dirac piece will be done separately elsewhere, when I get around to it, and contains the Rarita-Schwinger field content, which is fundamental and new.
02:41:27
There are only two generations in this model. I think people have accepted that there are three, but I don’t believe that there are three. I think that there are two, and that the third that unifies with other matter at higher energies.
02:41:39
The quartic Higgs piece comes from the Dirac squaring of a quadratic. Remember, there’s an eddy tensor, which is quadratic in the augmented torsion.
02:41:48
The metric does multiple duties. Here, it’s the main field in this version of GU, with the sort of strongest assumptions, as field content that is originally on \(X\), whereas most of the rest of the field content is on \(Y\), but it also acts as the observer pulling back the full content of \(Y\) onto \(X\), to be interpreted as if it came from \(X\) all along, generating the sort of illusion of internal quantum numbers.
02:42:20
And I should say that the Pati-Salam theory, which is usually advertised as, I think as \(\text{SU}(4) \times \text{SU}(2) \times \text{SU}(2)\), is really much more naturally \(\text{Spin}(6) \times \text{Spin}(4)\) when the trace portion of the space of metrics is put in with the proper sign if you’re trying to generate the sector that begins as \(X(1,3)\). Remember \(X^d\), where \(d = 4\), is the generic situation. But you have all these different sectors. I believe that these sectors probably exist if this model’s correct, but we are trapped in the \((1,3)\) sector, so you have to figure out what the implications are for pushing that indefinite signature up into an indefinite signature on the \(Y\) manifold. And, there are signatures that make it look like the Pati-Salam rather than directly in the \(\text{Spin}(10)\), \(\text{SU}(5)\) line of thinking.
Closing Thoughts

02:43:18
So we will attempt to present the full theory shortly. Keep in mind, this took seven years to just bring me to want to come back to this, but it must be reassembled from decades of notes, and that’s part of the problem when you’re working alone and you’re not really expecting to talk to anybody. So I want to thank you for your patience and your time, and I just want to read a bunch of names that people who mattered to me, and if I’ve done anything wrong, this is no reflection on them.
02:43:46
Marcus du Sautoy, Peter Thiel, Isadore Singer, Raoul Bott, Michael Grossberg, Adil Abdulali, Harry and Sophie Rubin, Bret Weinstein and family, Heather Heying, and Zach and Toby, Peter Freyd, Scott Axlerod, Nima Arkani-Hamed, Luis Alvarez Gaume, Edward Frankel, Dror Bar-Natan, Shlomo Sternberg, David Kazhdan, Daniel Barcay, Karen and Les Weinstein, Haynes Miller, Ralph Gomory, John Tate, Sidney Coleman, Graeme Segal, Robert Hermann, and Hira and Esther Malaney.
02:44:19
Errors and omissions, because I’ve too many people to thank, are all my own, as for the claims that should reflect badly on no one else other than myself.
02:44:30
And most especially, I just want to say that I’ve asked a tremendous amount from my family to stick with me on this quixotic quest. I want to thank Pia Malaney, Naila Weinstein, and Zev Weinstein. I love you all very much, and thank you for making this possible.


02:44:48
I do want to leave you with one thought. I really think that we’ve gotten completely bent out of shape about trying to formalize and routinize science, and it doesn’t work. You cannot mandate science as social engineering, you can’t decide that science is always in the zeitgeist and done by committee. In fact, it is essential to understand that science will not conform to what you want. One of the things that I’m very proud of, and I think is quite true, is the saying that great science has the scientific method as its radio edit. I don’t think that great science is actually done the way we say it’s done, and I think that Dirac’s 1963 Scientific American article should be read by absolutely everyone.
02:45:36
Every time major theories have come out, they’ve almost always been wrong, but they’re not wrong in an important way, and I think that we have to fix the political economy of people racing to correct theories or point out that there is no agreement with experiment. We are killing many of our best ideas by creating a terrible and combative environment, which already attempts to apportion credit for work, and more importantly, risk undertaken by individuals. And I just think that—I want people to understand that I’ve always wanted to share this, but I detest the culture that I saw that cropped up around what has now become known as the Seiberg-Witten equations. When they were put forward, there was a period of time where I watched people, as if at a feeding trough, trying to stay up around the clock to use a new machine tool that had been given to them to claim credit, and it profoundly pushed me away from the community. We have to become more ethical and we have to honor the people who are trying to speak and act imaginatively.
02:46:51
Now, if this doesn’t work, if it’s silly, I’ll have egg on my face and I’ll go on, I’ll be fine. But I’m very worried that maybe some of the best ideas are between the ears of people without the confidence, and the chutzpah, and just the, sort of, almost psychotic drive to push things across the finishing line. We’ve got to be kinder, and nicer, and more decent, and stop stealing people’s lives, their credit, their future, and their ability to have families and make a living, and that’s absolutely essential to me.
02:47:25
And, I look forward to finding out whether this theory has merit to it or is without merit, but I guarantee that if I’m going to go down with the ship, I’m also not going to be knocked off the ship as I was many years ago completely unfairly. And I won’t dwell on it, but the amount of power you professors have is absolutely, almost without parallel, because nobody really understands enough to adjudicate disputes that happen in academics. I’m going to insist that we fund you better, and that you are nicer to the people who depend upon you in this beautiful chain that we call scientific method, and most particularly, American science, which I think is still the envy of the world.
02:48:12
So you’ve been through The Portal, I know it was a long slog. I hope you found it interesting and enjoyable, and we’ll see you again soon. Be well everybody, stay safe.